题目内容
14.先化简,再求值:$\frac{a^3}{{{a^2}-2a+1}}÷({1-\frac{1}{1-a}})$,其中a2+a-1=0.分析 先把括号内通分后进行同分母的减法运算,再把除法运算化为乘法运算,接着约分得到原式=$\frac{{a}^{2}}{a-1}$,由于a2+a-1=0,则a2=-(a-1),然后利用整体代入的方法计算.
解答 解:原式=$\frac{{a}^{3}}{(a-1)^{2}}$÷$\frac{a-1+1}{a-1}$
=$\frac{{a}^{3}}{(a-1)^{2}}$•$\frac{a-1}{a}$
=$\frac{{a}^{2}}{a-1}$,
∵a2+a-1=0,
∴a2=-(a-1)
∴原式=$\frac{-(a-1)}{a-1}$=-1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
6.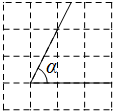 如图,在4×4的正方形网格中,tanα的值等于( )
如图,在4×4的正方形网格中,tanα的值等于( )
 如图,在4×4的正方形网格中,tanα的值等于( )
如图,在4×4的正方形网格中,tanα的值等于( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
15.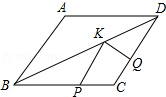 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
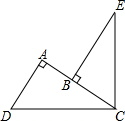 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.