题目内容
6.如图,将等腰Rt△ABC放置在平面直角坐标系中,∠CAB=90°,AC=AB.(1)如图1,点B,C分别在x,y轴上,求证:点A在∠BOC的角平分线上;
(2)如图2,已知A(3,0),C(0,4),求点B的坐标;
(3)如图3,点A,C分别在x,y轴上,点E为BC上一点,以AE为边作等腰Rt△AED,∠AED=90°,连接CD,求∠ACD的度数.

分析 (1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,证明A、B、O、C四点共圆,由圆周角定理得出∠AOC=∠ABC=45°,∠AOB=∠ACB=45°,即可得出结论;
(2)作BM⊥x轴于m,证出∠ABM=∠CAO,由AAS证明△ABM≌△ACO,得出BM=OA=3,AM=OC=4,求出OM=7,即可得出点B的坐标;
(3)由等腰直角三角形的性质得出∠ADE=45°=∠ACB,证出A、E、D、C四点共圆,由圆内接四边形的性质得出∠ACD+∠AED=180°,即可得出结果.
解答 (1)证明:∵∠CAB=90°,AC=AB,∴∠ABC=∠ACB=45°,
∵∠ACB+∠BOC=90°+90°=180°,
∴A、B、O、C四点共圆,
∴∠AOC=∠ABC=45°,∠AOB=∠ACB=45°,
∴∠AOC=∠AOB,
∴OA平分∠BOC,
即点A在∠BOC的角平分线上;
(2)解:∵A(3,0),C(0,4),
∴OA=3,OC=4,
作BM⊥x轴于M,如图所示: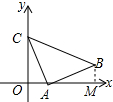 则∠BMA=90°=∠AOC,
则∠BMA=90°=∠AOC,
∴∠BAM+∠ABM=90°,
∵∠CAB=90°,
∴∠BAM+∠CAO=90°,
∴∠ABM=∠CAO,
在△ABM和△ACO中,
$\left\{\begin{array}{l}{∠ABM=∠CAO}&{\;}\\{∠BMA=∠AOC}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△ABM≌△ACO(AAS),
∴BM=OA=3,AM=OC=4,
∴OM=OA+AM=3+4=7,
∴点B的坐标为(7,3);
(3)解:∵△AED是等腰直角三角形,
∴∠AED=90°,∠ADE=45°=∠ACB,
∴A、E、D、C四点共圆,
∴∠ACD+∠AED=180°,
∴∠ACD=90°.
点评 本题考查了全等三角形的判定与性质、四点共圆、圆周角定理、等腰直角三角形的性质、圆内接四边形的性质等知识;本题综合性强,有一定难度.

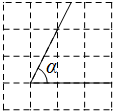 如图,在4×4的正方形网格中,tanα的值等于( )
如图,在4×4的正方形网格中,tanα的值等于( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
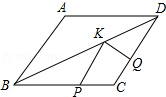 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
| A. | 0.096×106 | B. | 9.6×104 | C. | 9.6×108 | D. | 9.6×105 |
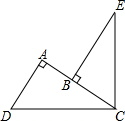 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.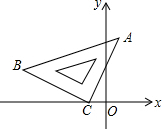 在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.
在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.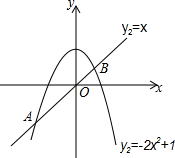 如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.
如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.