题目内容
4.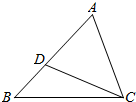 如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.
如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长.
分析 (1)根据相似三角形的判定得出即可;
(2)根据相似得出比例式,代入求出即可.
解答 (1)证明:∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC;
(2)解:∵△ACD∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AC2=AD×AB,
∵AD=6,AB=10,
∴AC=2$\sqrt{15}$.
点评 本题考查了相似三角形的性质和判定的应用,能求出△ACD∽△ABC是解此题的关键.

练习册系列答案
相关题目
15.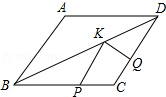 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
12.下列说法:①三点确定一个圆;②平分弦的直径必垂直于这条弦;③圆周角等于圆心角的一半;④等弧所对的圆心角相等;⑤各角相等的圆内接多边形是正多边形.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.我国的国土面积约为9.6×106平方千米,大约是韩国国土面积的100倍,则用科学记数法表示韩国的国土面积大约是(单位:千米)( )
| A. | 0.096×106 | B. | 9.6×104 | C. | 9.6×108 | D. | 9.6×105 |
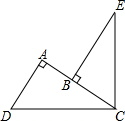 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.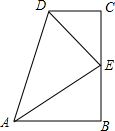 如图,四边形ABCD中,∠B=∠C=90°,∠CED=35°,DE平分∠ADC.
如图,四边形ABCD中,∠B=∠C=90°,∠CED=35°,DE平分∠ADC.