Question

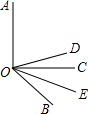已知：如图所示，∠AOB是钝角，OC、OD、OE是三条射线，OC⊥OA，OD平分∠AOB，OE平分∠BOC．请你求出∠DOE的度数．

Answer 1

考点：角的计算

专题：计算题

分析：设∠BOC=x°，则∠AOB=90°+x°，根据角平分线的定义即可表示出∠BOD和∠BOE的度数，根据∠DOE=∠BOD-∠BOE即可求解．

解答：解：设∠BOC=x°，则∠AOB=90°+x°，
∵OD平分∠AOB，
∴∠BOD=

1

2

（90-x）°，
∵OE平分∠BOC，
∴∠BOE=

1

2

x°，
∴∠DOE=∠BOD-∠BOE=

1

2

（90-x）°-

1

2

x°=45°．

点评：本题考查了角度的计算，正确设出未知数，表示出∠BOD和∠BOE的度数是关键．