题目内容
14．
如图，AB∥CD，如果∠1=110°，∠3=30°，那么∠2=100°．
分析 过E作EF∥AB，根据平行线的性质即可得到结论．
解答 
解：过E作EF∥AB，
∵AB∥CD，
∴EF∥CD，
∴∠1+∠BEF=180°，∠CEF=∠3=30°，
∴∠BEF=70°，
∴∠2=∠BEF+∠CEF=100°，
故答案为：100°．
点评 本题考查了平行线的性质，熟练掌握平行线的性质定理是解题的关键．
练习册系列答案
小夫子全能检测系列答案
相关题目
5．
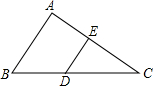如图，△ABC，点D在BC上，DE∥AB交AC于点E，如果$\frac{AE}{EC}=\frac{2}{3}$，那么$\frac{DE}{AB}$的值为（ ）
如图，△ABC，点D在BC上，DE∥AB交AC于点E，如果$\frac{AE}{EC}=\frac{2}{3}$，那么$\frac{DE}{AB}$的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
2．已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根，则该三角形的周长可以是（ ）
| A． | 5 | B． | 7 | C． | 5或7 | D． | 10 |
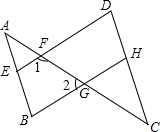如图，已知：∠A=∠C，∠B=∠D．你能确定图中∠1与∠2的数量关系吗？请写出你的结论并进行证明．
19．下列各数中，无理数是（ ）
| A． | $\sqrt{4}$ | B． | 3.14 | C． | $\root{3}{-27}$ | D． | 5π |
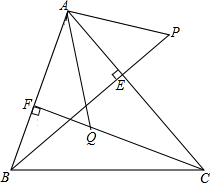如图，已知BE，CF是△ABC的高，P为BE延长线上的-点，Q为CF上一点，△PAB≌△AQC，且AB与QC是对应边，试说明AP⊥AQ．