题目内容
1.将矩形的各边中点顺次连接起来,所得的四边形是菱形.分析 作出图形,根据三角形的中位线定理可得EF=GH=$\frac{1}{2}$AC,FG=EH=$\frac{1}{2}$BD,再根据矩形的对角线相等可得AC=BD,从而得到四边形EFGH的四条边都相等,然后根据四条边都相等的四边形是菱形解答.
解答 解:如图,连接AC、BD,
∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点,
∴EF=GH=$\frac{1}{2}$AC,FG=EH=$\frac{1}{2}$BD(三角形的中位线等于第三边的一半),
∵矩形ABCD的对角线AC=BD,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
故答案为:菱形.
点评 本题考查了三角形的中位线定理,菱形的判定,矩形的性质,作辅助线构造出三角形,然后利用三角形的中位线定理是解题的关键.

练习册系列答案
相关题目
6.已知菱形的边长和一条对角线的长均为2,菱形的面积为( )
| A. | 4 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
13.若最简二次根式3$\sqrt{5}$与-5$\sqrt{x}$可以合并,则x的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
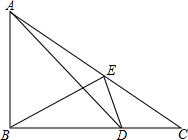 如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.
如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.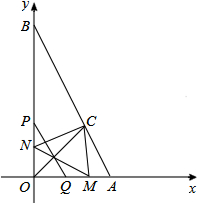 如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.
如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.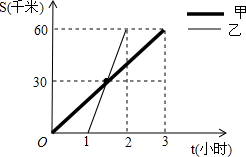 甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空: