题目内容
6.已知菱形的边长和一条对角线的长均为2,菱形的面积为( )| A. | 4 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
分析 由四边形ABCD是菱形,可得菱形的四条边都相等AB=BC=CD=AD,菱形的对角线互相平分且相等即AC⊥BD,OA=OC,OB=OD,又因为菱形的边长和一条对角线的长均为2,易求得OB=1,则可得AC的值,根据菱形的面积等于积的一半,即可求得菱形的面积.
解答 解:根据题意画出图形,如图所示: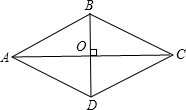
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=2cm,AC⊥BD,OA=OC,OB=OD,
又∵菱形的边长和一条对角线的长均为2,
∴AB=AD=BD=2,
∴OB=1,
∴OA=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∴菱形的面积为2$\sqrt{3}$,
故选C.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
14.我们可以把|x-y|理解为数轴上表示x的点到表示y的点距离.若2≤x≤4,则|x+1|+|x-2|+|x-3|的最小值和最大值分别为( )
| A. | 4,8 | B. | 4,9 | C. | 5,8 | D. | 5,9 |
18.下列句子不是真命题的是( )
| A. | 两直线平行,同位角相等 | B. | 同旁内角互补,两直线平行 | ||
| C. | 若a2=b2,则a=b | D. | 对顶角相等 |
15.下列各线中,不属于等腰三角形“三线合一”的线是( )
| A. | 顶角的平分线 | B. | 底边上的中线 | C. | 底边上的中垂线 | D. | 底边上的高线 |