题目内容
9.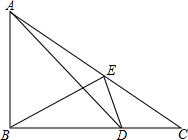 如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.
如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.(1)求证:DE2+BE2=DB2;
(2)已知DE=2,求BE的长.
分析 (1)利用等量代换得出∠BDE=90°,利用勾股定理得出结论;
(2)作∠BAC的平分线交BE于点H,证得BH=EH=$\frac{1}{2}$BE,RT△ABE≌RT△BDE,进一步得出结论即可.
解答 (1)证明:∵∠ABC=90°,
∴∠ABE+∠EBC=90°,
∵∠ABE=∠BDE,
∴∠BDE+∠EBC=90°,
∴∠BED=90°,
∴DE2+BE2=DB2.
(2)解:如图,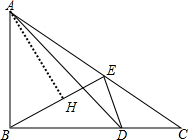
作∠BAC的平分线交BE于点H,则∠BAC=2∠BAH,
∵∠ABC=90°,
∴∠BAC+∠C=90°,
∵∠C+2∠EBC=90°,
∴∠EBC=∠BAH,
∵∠EBC+∠ABE=∠ABC=90°,
∴∠BAH+∠ABE=90°,
∴∠AHB=90°=∠BED,BH=EH=$\frac{1}{2}$BE,
在RT△ABH与RT△BDE中,
$\left\{\begin{array}{l}{AB=BD}\\{∠AHB=∠BED}\\{∠BAH=∠DBE}\end{array}\right.$,
∴RT△ABH≌RT△BDE,
∴BH=DE=2,
∴BE=2BH=4.
点评 此题考查全等三角形的判定与性质,勾股定理,搞清角与边之间的数量关系解决问题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
14.我们可以把|x-y|理解为数轴上表示x的点到表示y的点距离.若2≤x≤4,则|x+1|+|x-2|+|x-3|的最小值和最大值分别为( )
| A. | 4,8 | B. | 4,9 | C. | 5,8 | D. | 5,9 |
18.下列句子不是真命题的是( )
| A. | 两直线平行,同位角相等 | B. | 同旁内角互补,两直线平行 | ||
| C. | 若a2=b2,则a=b | D. | 对顶角相等 |
19.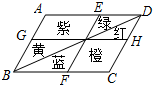 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )| A. | 球落在红花丛中和绿花丛中的概率相等 | |
| B. | 球落在紫花丛中和橙花丛中的概率相等 | |
| C. | 球落在红花丛中和蓝花丛中的概率相等 | |
| D. | 球落在蓝花丛中和黄花丛中的概率相等 |
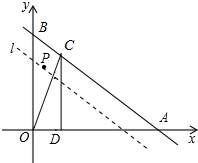 如图,已知点A(6$\sqrt{3}$,0),点B(0,6),经过AB的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,已知点A(6$\sqrt{3}$,0),点B(0,6),经过AB的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.