题目内容
 如图,在⊙O中,OA是半径,AB,AC是弦,且
如图,在⊙O中,OA是半径,AB,AC是弦,且 |
| AB |
 |
| AC |
考点:圆心角、弧、弦的关系
专题:证明题
分析:根据圆心角、弧、弦的关系得到∠AOB=∠AOC,再根据“SAS”证明△AOB≌△AOC,则可得到∠OAB=∠OAC,然后根据角平分线的定义即可得到结论.
解答:
解:∵
=
,
∴∠AOB=∠AOC,
在△AOB和△AOC中,
,
∴△AOB≌△AOC,
∴∠OAB=∠OAC,
∴点O在∠BAC的平分线上.
 |
| AB |
 |
| AC |
∴∠AOB=∠AOC,
在△AOB和△AOC中,
|
∴△AOB≌△AOC,
∴∠OAB=∠OAC,
∴点O在∠BAC的平分线上.
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
随着锐角α的增大,cosα的值( )
| A、增大 | B、减小 |
| C、不变 | D、增大还是减小不确定 |
 如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=8,ED=2,AC=3,则AB的长是( )
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=8,ED=2,AC=3,则AB的长是( )| A、5 | B、6 | C、7 | D、8 |
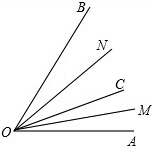 如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线
如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线 如图,四边形ABCD内接于⊙O,∠B=∠D,如果AB=3,BC=4,那么⊙O的半径等于
如图,四边形ABCD内接于⊙O,∠B=∠D,如果AB=3,BC=4,那么⊙O的半径等于 如图,已知∠ADE=70°,DF平分∠ADE,∠1=35°,求证:DF∥BE.
如图,已知∠ADE=70°,DF平分∠ADE,∠1=35°,求证:DF∥BE. 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(0,0)表示A点的位置,用(4,-1)表示B点的位置,那么:
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(0,0)表示A点的位置,用(4,-1)表示B点的位置,那么: