题目内容
18. 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF;
(3)若AB=6,AD=12,求△BEF的面积.
分析 (1)根据平行线的性质、翻转变换的性质解答;
(2)根据等腰三角形的性质证明;
(3)根据翻转变换的性质、勾股定理计算即可.
解答 解:(1)∵AD∥BC,
∴∠2=∠1=60°,
由翻转变换的性质可知,∠BEF=∠2=60°,
∴∠3=60°;
(2)证明:∵∠BEF=∠1=60°,
∴BE=BF;
(3)由翻转变换的性质可知,BE=DE=12-AE,
由勾股定理得,BE2=AB2+AE2,即(12-AE)2=62+AE2,
解得,AE=4.5,
则BF=BE=7.5,
∵四边形ABHE是矩形,
∴EH=AB=6,
∴△BEF的面积=$\frac{1}{2}$×BF×EH=22.5.
点评 本题考查的是翻转变换的性质,翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
9.下面条件中,不能证出Rt△ABC≌Rt△A'B'C'的是( )
| A. | AC=A'C',BC=B'C' | B. | AB=A'B',AC=A'C' | C. | AB=B'C',AC=A'C' | D. | ∠B=∠B',AB=A'B' |
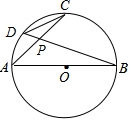 已知:如图AB为⊙O的直径,弦AC、BD相交于点P,
已知:如图AB为⊙O的直径,弦AC、BD相交于点P, 如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).
如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).