题目内容
19. 在下列推理过程中的括号里填上推理的依据.
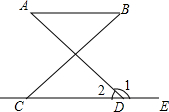
在下列推理过程中的括号里填上推理的依据.已知:如图,CDE是直线,∠1=105°,∠A=75°.
求证:AB∥CD.
证明:∵CDE为一条直线(已知)
∴∠1+∠2=180°
∵∠1=105°(已知)
∴∠2=75°
又∵∠A=75°(已知)
∴∠2=∠A(等量代换)
∴AB∥CD(内错角相等两直线平行)
分析 首先根据平角定义可得∠1+∠2=180,然后可计算出∠2的度数,从而可得∠2=∠A,再根据内错角相等,两直线平行可得AB∥CD.
解答 证明:∵CDE为一条直线(已知),
∴∠1+∠2=180°
∵∠1=105°(已知)
∴∠2=75°
又∵∠A=75°(已知)
∴∠2=∠A(等量代换)
∴AB∥CD(内错角相等两直线平行)
故答案为:已知;等量代换;内错角相等两直线平行.
点评 此题主要考查了平行线的判定,关键是掌握平行线的判定方法:内错角相等两直线平行.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.6把钥匙有2把是开大门和房门的(钥匙大小都相同),某人在黑夜摸出钥匙开门,则他一次成功地打开两道门的概率是(打开大门后钥匙不放回)( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
10.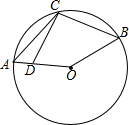 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )| A. | ∠DCB+$\frac{1}{2}$∠O=180° | B. | ∠ACB+$\frac{1}{2}$∠O=180° | C. | ∠ACB+∠O=180° | D. | ∠CAO+∠CBO=180° |
8.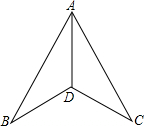 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |
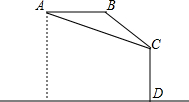 如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.
如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.