题目内容
9.在△ABC中,AB=AC,∠BCD=∠BAC,点D与点A在BC的两侧,∠BCD的边CD所在的直线与边AB坐在的直线相交于点P,PE⊥AC,垂足为E.若∠BAC=90°时,如图(1)易证2CE=AP+AB;
若∠BAC≠90°时,其他条件不变,如图(2)、图(3),则在图(2)、图(3)两种情况下线段CE、AP、AB又有怎样的数量关系?请直接写出你的猜想,并对其中一种情况给予证明.
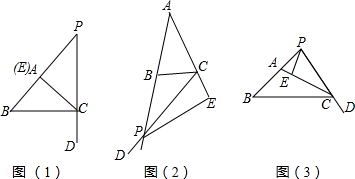
分析 根据等腰三角形三线合一的性质进行分析得出线段CE、AP、AB的关系即可.
解答 解:如图1:过点P作PF∥BC,交AC的延长线于点F,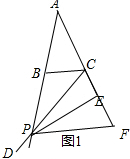
∴∠APF=∠ABC=∠ACB=∠F,
∴AF=AP,
∵∠BCF=∠A+∠ABC,
∴∠PCF+∠BCD=∠A+∠ABC,
∵∠BCD=∠A,
∴∠PCF=∠ABC,
∴∠PCF=∠F,
∴PC=PF,
∵PE⊥CF,
∴CE=EF(三线合一),
∴2CE=CF=AF-AC=AP-AB;
如图2,过点P作PF∥BC,交CA的延长线于点F,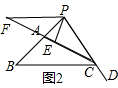
∴∠APF=∠B=∠ACB=∠F,
∴AF=AP,
∵∠BCD=∠BPC+∠B,
∠BAC=∠BPC+∠PCF,
∠BCD=∠BAC,
∴∠B=∠PCF,
∴∠PCF=∠F,
∴PC=PF,
∵PE⊥CF,
∴CE=EF(三线合一),
∴2CE=CF=AF+AC=AP+AB.
点评 此题考查全等三角形问题,关键是根据等腰三角形的三线合一的性质解答.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
12.一元二次方程x2-2x=0的根是( )
| A. | x1=0,x2=-2 | B. | x1=1,x2=2 | C. | x1=1,x2=-2 | D. | x1=0,x2=2 |
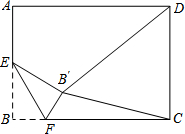 如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.
如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.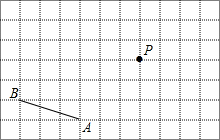 如图,在7×11网格中,已知线段AB和点P,按下列要求画图.
如图,在7×11网格中,已知线段AB和点P,按下列要求画图.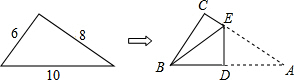 如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.
如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.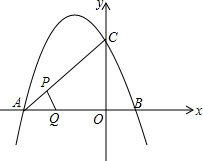 如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.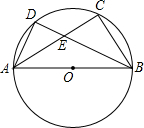 如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DC}$,AB=10,BD=8,则AE=$\frac{15}{2}$.
如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DC}$,AB=10,BD=8,则AE=$\frac{15}{2}$. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )