题目内容
19. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )| A. | 10 | B. | 7 | C. | 5 | D. | 4 |
分析 作EF⊥BC于F,根据角平分线的性质求得EF=DE=2,然后根据三角形面积公式求得即可.
解答 解:作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=$\frac{1}{2}$BC•EF=$\frac{1}{2}$×5×2=5,
故选C.
点评 本题考查了角的平分线的性质以及三角形的面积,作出辅助线求得三角形的高是解题的关键.

练习册系列答案
相关题目
10.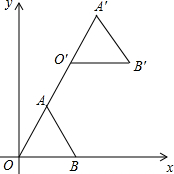 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )| A. | (4,2$\sqrt{3}$) | B. | (3,3$\sqrt{3}$) | C. | (4,3$\sqrt{3}$) | D. | (3,2$\sqrt{3}$) |
11.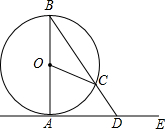 如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
 如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 20° |
8.一个不透明的布袋中,放有3个白球,5个红球,它们除颜色外完全相同,从中随机摸取1个,摸到红球的概率是( )
| A. | $\frac{5}{8}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{3}$ |
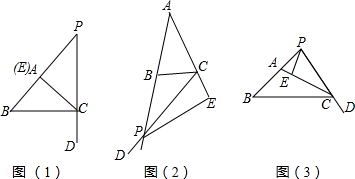

 将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )