题目内容
13.已知实数m,n满足3m2+6m-5=0,3n2+6n-5=0,且m≠n,则$\frac{n}{m}$$+\frac{m}{n}$=-$\frac{22}{5}$.分析 由m≠n时,得到m,n是方程3x2+6x-5=0的两个不等的根,根据根与系数的关系进行求解.
解答 解:∵m≠n时,则m,n是方程3x2+6x-5=0的两个不相等的根,∴m+n=-2,mn=-$\frac{5}{3}$.
∴原式=$\frac{{m}^{2}{+n}^{2}}{mn}$=$\frac{{(m+n)}^{2}-2mn}{mn}$=$\frac{(-2)^{2}-2×(-\frac{5}{3})}{-\frac{5}{3}}$=-$\frac{22}{5}$,
故答案为:-$\frac{22}{5}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.计算:|-5+3|的结果是( )
| A. | -2 | B. | 2 | C. | -8 | D. | 8 |
8.某班45名同学某天每人的生活费用统计如表:
对于这45名同学这天每人的生活费用,下列说法错误的是( )
| 生活费(元) | 10 | 15 | 20 | 25 | 30 |
| 学生人数(人) | 4 | 10 | 15 | 10 | 6 |
| A. | 平均数是20 | B. | 众数是20 | C. | 中位数是20 | D. | 极差是20 |
5.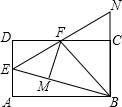 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.
其中,正确的结论有( )
 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.
其中,正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.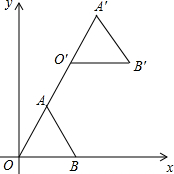 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )| A. | (4,2$\sqrt{3}$) | B. | (3,3$\sqrt{3}$) | C. | (4,3$\sqrt{3}$) | D. | (3,2$\sqrt{3}$) |
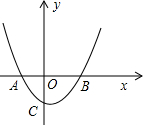 如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.