题目内容
已知，如图，BC是圆O的直径，A是弦BD延长线上一点，AC⊥BC于点C，切线DE交AC于点E．（1）求证：AE=EC．
（2）若AD=DB，OC=5，求切线AC的长．
考点：切线的性质
专题：
分析：（1）连接CD，则DE=EC，∠EDC=∠ECD，且∠A+∠ECD=90°，∠ADE+∠EDC=90°，可证得EA=ED，所以可得AE=EC；
（2）当BD=AD时，可知AC=BC=2OC=10．
（2）当BD=AD时，可知AC=BC=2OC=10．
解答：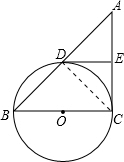
（1）证明：如图，连接CD，
∵AC⊥BC，
∴AC为⊙O的切线，
∵DE为⊙的切线，
∴DE=EC，
∴∠EDC=∠ECD，
∵BC为直径，
∴∠ADC=90°，
∴∠A+∠ECD=90°，∠EDA+∠EDC=90°，
∴∠A=∠EDA，
∴DE=AE，
∴AE=EC；
（2）解：∵AD=BD，且CD⊥AB，
∴CD为AB的垂直平分线，
∴AC=BC=2OC=10．
（1）证明：如图，连接CD，∵AC⊥BC，
∴AC为⊙O的切线，
∵DE为⊙的切线，
∴DE=EC，
∴∠EDC=∠ECD，
∵BC为直径，
∴∠ADC=90°，
∴∠A+∠ECD=90°，∠EDA+∠EDC=90°，
∴∠A=∠EDA，
∴DE=AE，
∴AE=EC；
（2）解：∵AD=BD，且CD⊥AB，
∴CD为AB的垂直平分线，
∴AC=BC=2OC=10．
点评：本题主要考查圆的切线的判定和性质及切线长定理、线段垂直平分线的判定和性质，掌握切线长定理及切线的判定和性质是解题的关键，在该题中得到ED=EA是解题的关键．
练习册系列答案
相关题目
几何体简称为体，按其形状可分为三类，即柱体、椎体、球体，下列图形中：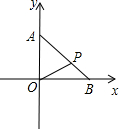
如图，点B，A分别在x，y轴的正半轴上，AB=m，且AP：PB=2：1，点B在x轴的正半轴上移动，线段AB的长保持不变．