题目内容
在△ABC中,AD平分∠BAC,AB>AC,CE⊥AD,E为垂足,求证:∠ECD=
(∠ACB-∠B)
| 1 |
| 2 |
考点:三角形内角和定理
专题:证明题
分析:首先根据三角形的内角和定理及直角三角形的性质,求出∠ACE与∠B和∠ACB之间的关系,即可解决问题.
解答: 解:如图,
解:如图,
∵AD平分∠BAC,
∴∠BAD=∠CAD=
∠BAC=
(180°-∠B-∠ACB)=90°-
(∠B+∠ACB);
∵CE⊥AD,
∴∠ACE=90°-∠CAD=
(∠B+∠ACB),
∴∠ECD=∠ACB-∠ACE=
(∠ACB-∠B),即∠ECD=
(∠ACB-∠B).
 解:如图,
解:如图,∵AD平分∠BAC,
∴∠BAD=∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵CE⊥AD,
∴∠ACE=90°-∠CAD=
| 1 |
| 2 |
∴∠ECD=∠ACB-∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:该命题主要考查了三角形的内角和定理及其应用问题;解题的关键是灵活运用有关定理来进行分析、判断、推理或解答.

练习册系列答案
相关题目
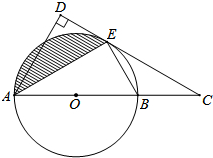 如图,已知AB为⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD,垂足为D.
如图,已知AB为⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD,垂足为D. 已知,如图,BC是圆O的直径,A是弦BD延长线上一点,AC⊥BC于点C,切线DE交AC于点E.
已知,如图,BC是圆O的直径,A是弦BD延长线上一点,AC⊥BC于点C,切线DE交AC于点E. 画出如图所示的几何体的三视图.
画出如图所示的几何体的三视图.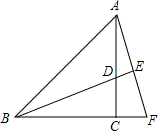 如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.
如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.