题目内容
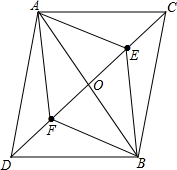 已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形.
已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形.考点:平行四边形的判定
专题:证明题
分析:通过全等三角形(△AOC≌△BOD)的对应边相等推知:AC=BD,结合已知条件AC∥DB可以证得结论.
解答: 证明:如图,∵AC∥DB,
证明:如图,∵AC∥DB,
∴∠ACO=∠BDO.
在△AOC与△BOD中,∵
,
∴△AOC≌△BOD(AAS),
∴AC=BD,
∴四边形ADBC是平行四边形.
 证明:如图,∵AC∥DB,
证明:如图,∵AC∥DB,∴∠ACO=∠BDO.
在△AOC与△BOD中,∵
|
∴△AOC≌△BOD(AAS),
∴AC=BD,
∴四边形ADBC是平行四边形.
点评:本题考查了平行四边形的判定.此题利用“一组对边平行且相等的四边形是平行四边形”证得结论.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、等底等高的两个三角形全等 |
| B、周长相等的直角三角形都全等 |
| C、有两边和一角对应相等的两个三角形全等 |
| D、有一边对应相等的两个等边三角形全等 |
 以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么?
以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么?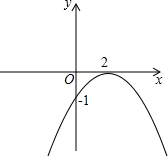 如图是y=a(x+m)2的图象
如图是y=a(x+m)2的图象 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG. 如图,点D、E分别在△ABC的边AB、AC上,BE、CD相交于点O,∠1=∠2,连接DE,图中共有多少对相似三角形?请把它们写出来.
如图,点D、E分别在△ABC的边AB、AC上,BE、CD相交于点O,∠1=∠2,连接DE,图中共有多少对相似三角形?请把它们写出来. 在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有多少条?
在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有多少条?