题目内容
17.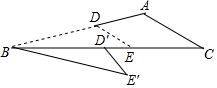 如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为2+$\sqrt{34}$.
如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为2+$\sqrt{34}$.
分析 根据旋转可得BE=BE'=5,BD=BD',进而得到BD=BC-4,再根据平行线分线段成比例定理,即可得到$\frac{BD}{BA}$=$\frac{BE}{BC}$,即$\frac{BC-4}{6}$=$\frac{5}{BC}$,即可得出BC的长.
解答  解:由旋转可得,BE=BE'=5,BD=BD',
解:由旋转可得,BE=BE'=5,BD=BD',
∵D'C=4,
∴BD'=BC-4,即BD=BC-4,
∵DE∥AC,
∴$\frac{BD}{BA}$=$\frac{BE}{BC}$,即$\frac{BC-4}{6}$=$\frac{5}{BC}$,
解得BC=2+$\sqrt{34}$(负值已舍去),
即BC的长为2+$\sqrt{34}$.
故答案为:2+$\sqrt{34}$.
点评 本题主要考查了旋转的性质,解一元二次方程以及平行线分线段成比例定理的运用,解题时注意:对应点到旋转中心的距离相等.解决问题的关键是依据平行线分线段成比例定理,列方程求解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.下列图案中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.如图,在平面直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△AOB连续旋转变换,依次得到△1,△2,△3,△4…,则△2017的直角顶点的坐标为( )


| A. | (4032,0) | B. | (4036,0) | C. | (8064,0) | D. | (8068,0) |
17.已知函数y=(m+1)x+m的函数值y随自变量x的增大而减小,那么m的取值范围是( )
| A. | m>-1 | B. | m<-1 | C. | m<1 | D. | m<0 |
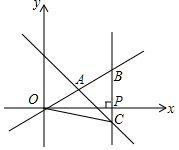 在平面直角坐标系xOy中,一次函数y=-x+7的图象交y轴于点D,且它与正比例函数y=$\frac{3}{4}$x的图象交于点A.
在平面直角坐标系xOy中,一次函数y=-x+7的图象交y轴于点D,且它与正比例函数y=$\frac{3}{4}$x的图象交于点A.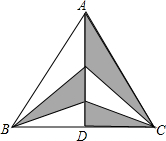 如图,AD所在的直线是△ABC的对称轴,若BC=6,AD=5,则图中阴影部分的面积和为7.5.
如图,AD所在的直线是△ABC的对称轴,若BC=6,AD=5,则图中阴影部分的面积和为7.5. 如图,转盘中6个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,指针指向奇数的概率是$\frac{2}{3}$.
如图,转盘中6个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,指针指向奇数的概率是$\frac{2}{3}$.