题目内容
8.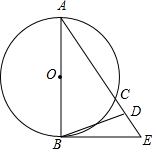 如图,AB是⊙O的直径,点C在圆上,D,E是AC的延长线上的点,连接BD交⊙O于点F,且∠BAD=2∠DBE,AB=AD.
如图,AB是⊙O的直径,点C在圆上,D,E是AC的延长线上的点,连接BD交⊙O于点F,且∠BAD=2∠DBE,AB=AD.(1)求证:BE是⊙O的切线;
(2)若AC=4,DE=1,求线段BD的长.
分析 (1)根据已知条件得到∠DBE=$\frac{∠BAD}{2}$,根据等腰三角形的性质和三角形的内角和得到∠ABD=∠ADB=$\frac{1}{2}$(180°-∠BAD)=90°-$\frac{∠BAD}{2}$=90°-∠DBE,于是得到结论;
(2)连接BC,由AB是⊙O的直径,得到∠ACB=90°,根据BE是⊙O的切线得到∠ABE=90°,设CD=x,则AB=AD=4+x,AE=5+x,由射影定理列方程即可得到结论.
解答  (1)证明:∴∠BAD=2∠DBE,
(1)证明:∴∠BAD=2∠DBE,
∴∠DBE=$\frac{∠BAD}{2}$,
∵AB=AD,
∴∠ABD=∠ADB=$\frac{1}{2}$(180°-∠BAD)=90°-$\frac{∠BAD}{2}$=90°-∠DBE,
∴∠ABD+∠DBE=90°-∠DBE+∠DBE=90°,
∴AB⊥BE,
∴BE是⊙O的切线;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵BE是⊙O的切线
∴∠ABE=90°,
设CD=x,则AB=AD=4+x,AE=5+x,
由射影定理得:AB2=AC•AE,
即(4+x)2=4(x+5),
解得:x=2(舍去负值),
∴BC2=AB2-AC2=(4+2)2-42=20,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{20+{2}^{2}}$=2$\sqrt{6}$.
点评 本题考查了切线的判定和性质,等腰三角形的性质,射影定理,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
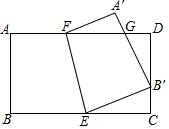 如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.
如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.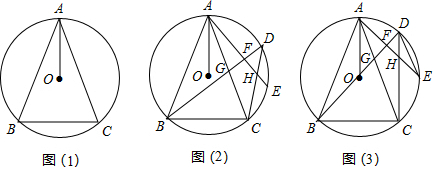
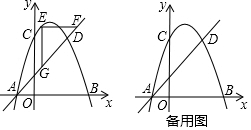
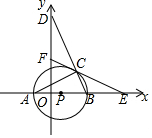 如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(-1,0)C(3,2$\sqrt{2}$),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(-1,0)C(3,2$\sqrt{2}$),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.