题目内容
20.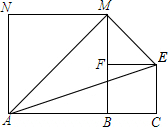 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2.
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2.
分析 将△AME的面积表示为长方形减去三个三角形的形式,根据题意,找出各边长度,根据长方形的面积,三角形的面积公式即可得出结论.
解答 解: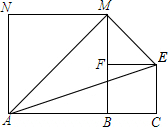 S△AME=AC•AN-$\frac{1}{2}$AN•MN-$\frac{1}{2}$AC•CE-$\frac{1}{2}$EF•MF.
S△AME=AC•AN-$\frac{1}{2}$AN•MN-$\frac{1}{2}$AC•CE-$\frac{1}{2}$EF•MF.
∵AB=n,BC=1,四边形ABMN及四边形BCEF均为正方形,
∴AN=MN=AB=n,EF=CE=BC=1,MF=BM-BF=n-1.
∴Sn=n(n+1)-$\frac{1}{2}$n•n-$\frac{1}{2}$(n+1)-$\frac{1}{2}$(n-1)=$\frac{1}{2}$n2.
故答案为:$\frac{1}{2}$n2
点评 本题考查了正方形的性质、长方形和三角形的面积公式,解题的关键是将△AME的面积表示为长方形减去三个三角形的形式.本题属于中档题,有点难度,由于△AMF不是特殊的三角形,故不能直角找出它的面积,需要利用分割长方形的方法才能得到结论.

练习册系列答案
相关题目
11.用放大镜将图形放大,应属于哪一种变换( )
| A. | 对称变换 | B. | 平移变换 | C. | 旋转变换 | D. | 相似变换 |
5.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
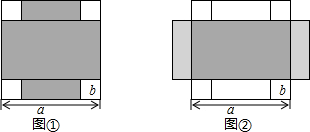

| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
12.将抛物线y=x2+5向右平移1个单位长度,再向下平移2个单位长度,后,得到的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
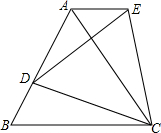 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.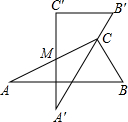 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.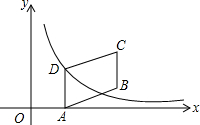 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.