题目内容
16.过圆O内一点P的最长的弦,最短弦的长度分别是8cm,6cm,则OP=$\sqrt{7}$cm.分析 根据直径是圆中最长的弦,知该圆的直径是8cm;最短弦即是过点P且垂直于过点P的直径的弦;根据垂径定理即可求得CP的长,再进一步根据勾股定理,可以求得OP的长.
解答 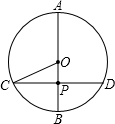 解:如图所示,直径AB⊥弦CD于点P,
解:如图所示,直径AB⊥弦CD于点P,
根据题意,得AB=8cm,CD=6cm,OC=$\frac{1}{2}$AB=4cm,
∵CD⊥AB,
∴CP=$\frac{1}{2}$CD=3cm.
根据勾股定理,得OP=$\sqrt{O{C}^{2}-C{P}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$(cm),
故答案为:$\sqrt{7}$cm.
点评 本题考查了垂径定理和勾股定理的应用,能根据垂径定理得出CP=$\frac{1}{2}$CD是解此题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6. 如图:在△ABC中,MN∥BC,若BM=4AM,MN=1,则BC的长是( )
如图:在△ABC中,MN∥BC,若BM=4AM,MN=1,则BC的长是( )
 如图:在△ABC中,MN∥BC,若BM=4AM,MN=1,则BC的长是( )
如图:在△ABC中,MN∥BC,若BM=4AM,MN=1,则BC的长是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
8. 如图,直线AB、CD相交于点O,OA⊥OE,则∠1和∠2的关系是( )
如图,直线AB、CD相交于点O,OA⊥OE,则∠1和∠2的关系是( )
 如图,直线AB、CD相交于点O,OA⊥OE,则∠1和∠2的关系是( )
如图,直线AB、CD相交于点O,OA⊥OE,则∠1和∠2的关系是( )| A. | 相等 | B. | 互补 | C. | 互余 | D. | 以上三种都不是 |
2.下列各组数中,能构成直角三角形的一组是( )
| A. | 6,8,12 | B. | 1,4,$\sqrt{3}$ | C. | 3,4,5 | D. | 2,2,$\sqrt{5}$ |
 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,s)、N(t,8)分别是边AB、BC上的两个动点,且OM⊥MN,当ON最小时,s+t=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,s)、N(t,8)分别是边AB、BC上的两个动点,且OM⊥MN,当ON最小时,s+t=10.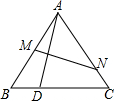 如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$. 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.