题目内容
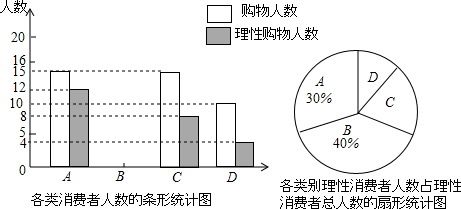
7. 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,s)、N(t,8)分别是边AB、BC上的两个动点,且OM⊥MN,当ON最小时,s+t=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,s)、N(t,8)分别是边AB、BC上的两个动点,且OM⊥MN,当ON最小时,s+t=10.
分析 易证得△OAM∽MBN,则$\frac{OA}{MB}=\frac{AM}{BN}$,由此可求得s与t的关系式,从而得到t的取值范围.由勾股定理可得ON=$\sqrt{O{C}^{2}+C{N}^{2}}$=$\sqrt{64+{t}^{2}}$,结合t的取值范围可得ON的最小值,从而求得s、t的值.
解答 解:∵∠OMN=∠B=∠A=90°,
∴∠NMB+∠MNB=90°,∠NMB+∠OMA=90°,
∴∠MNB=∠OMA,
∴△OAM∽MBN,
∴$\frac{OA}{MB}=\frac{AM}{BN}$,
即$\frac{8}{8-s}=\frac{s}{8-t}$,
所以(8-s)s=8(8-t),变形得(s-4)2=8t-48.
∵(s-4)2≥0,
∴8t-48≥0,t≥6.
∵ON=$\sqrt{O{C}^{2}+C{N}^{2}}$=$\sqrt{64+{t}^{2}}$,
当t=6时,ON取得最小值,最小值为$\sqrt{64+36}$=10.
将t=6代入(s-4)2=8t-48得s=4.
所以当ON最小时,s+t=6+4=10.
故答案为:10.
点评 本题考查了正方形的性质,相似三角形的判断,判断出t的取值范围是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
2.已知$\frac{x}{y}$=$\frac{3}{2}$,那么下列等式中一定正确的是( )
| A. | $\frac{3x}{y}$=$\frac{9}{2}$ | B. | $\frac{x+3}{y+3}$=$\frac{6}{5}$ | C. | $\frac{x-3}{y-2}$=$\frac{3}{2}$$•\frac{x}{y}$ | D. | $\frac{x+y}{x}$=$\frac{5}{2}$ |
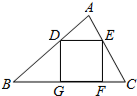 如图,△ABC中,点D、E是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形,若DE=2cm,求△ABC的面积.
如图,△ABC中,点D、E是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形,若DE=2cm,求△ABC的面积.
 如图,矩形ABCD中,点E是边AD的中点,BE交对角线AC于点F,则△AFE与△BCF的面积比等于$\frac{1}{4}$.
如图,矩形ABCD中,点E是边AD的中点,BE交对角线AC于点F,则△AFE与△BCF的面积比等于$\frac{1}{4}$.