题目内容
已知直线y=2x+a与直线y=-x+b都经过点A(-3,0),并且直线y=2x+a与y轴交于点B,直线y=-x+b与y轴交于点C,请你在同一直线坐标系中画出这两条直线并求△ABC的面积.
考点:两条直线相交或平行问题
专题:计算题
分析:先把A点坐标代入y=2x+a、y=-x+b可求出a、b的值,从而确定两直线解析式分别为y=2x+6,y=-x-3,于是可画出两函数图象,然后根据y轴上点的坐标特征确定B点和C点坐标,再利用三角形面积公式求解.
解答: 解:把A(-3,0)分别代入y=2x+a、y=-x+b得-6+a=0,3+b=0,解得a=6,b=-3,
解:把A(-3,0)分别代入y=2x+a、y=-x+b得-6+a=0,3+b=0,解得a=6,b=-3,
所以两直线解析式分别为y=2x+6,y=-x-3,
如图,
把x=0代入y=2x+6得y=6,则B点坐标为(0,6);把x=0代入y=-x-3得y=-3,则C点坐标为(0,-3),
所以S△ABC=
×3×(6+3)=
.
 解:把A(-3,0)分别代入y=2x+a、y=-x+b得-6+a=0,3+b=0,解得a=6,b=-3,
解:把A(-3,0)分别代入y=2x+a、y=-x+b得-6+a=0,3+b=0,解得a=6,b=-3,所以两直线解析式分别为y=2x+6,y=-x-3,
如图,
把x=0代入y=2x+6得y=6,则B点坐标为(0,6);把x=0代入y=-x-3得y=-3,则C点坐标为(0,-3),
所以S△ABC=
| 1 |
| 2 |
| 27 |
| 2 |
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
计算8a3÷(-2a)的结果是( )
| A、4a |
| B、-4a |
| C、4a2 |
| D、-4a2 |
 如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是
如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是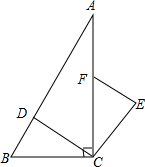 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.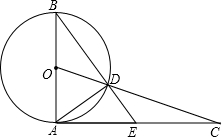 如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD. 如图,抛物线y=-
如图,抛物线y=-