题目内容
甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 0.4 | |
| 乙 | 9 | 3.2 |
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差
考点:方差,算术平均数,中位数,众数
专题:计算题
分析:(1)根据众数、平均数和中位数的定义求解;
(2)根据方差的意义求解;
(3)根据方差公式求解.
(2)根据方差的意义求解;
(3)根据方差公式求解.
解答:解:(1)甲的众数为8,乙的平均数=
×(5+9+7+10+9)=8,乙的中位数为9;
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
故答案为:8,8,9;变小.
| 1 |
| 5 |
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
故答案为:8,8,9;变小.
点评:本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差通常用s2来表示,计算公式是:s2=
[(x1-x?)2+(x2-x?)2+…+(xn-x?)2];方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了算术平均数、中位数和众数.
| 1 |
| n |

练习册系列答案
相关题目
方程x+2y=5的正整数解的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.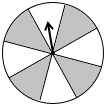 有一个能自由转动的转盘如图,盘面被分成8个大小与性状都相同的扇形,颜色分为黑白两种,将指针的位置固定,让转盘自由转动,当它停止后,指针指向白色扇形的概率是
有一个能自由转动的转盘如图,盘面被分成8个大小与性状都相同的扇形,颜色分为黑白两种,将指针的位置固定,让转盘自由转动,当它停止后,指针指向白色扇形的概率是