��Ŀ����
 ��ͼ��������y=-
��ͼ��������y=-| 1 |
| 2 |
��1���������ߵı���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��3����E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱE������꣮
���㣺���κ����ۺ���
ר�⣺���������ۺ���,ѹ����
��������1���ɴ���ϵ����������Ԫһ�η�����������m��n��ֵ���ɣ�
��2���ɣ�1���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����P1���Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�P2��P3����CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
��3�������BC�Ľ���ʽ�����E�������Ϊ��a��-
a+2�����Ϳ��Ա�ʾ��F�����꣬���ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
��2���ɣ�1���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����P1���Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�P2��P3����CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
��3�������BC�Ľ���ʽ�����E�������Ϊ��a��-
| 1 |
| 2 |
��� �⣺��1����������y=-
�⣺��1����������y=-
x2+mx+n����A��-1��0����C��0��2����
��ã�
��
�������ߵĽ���ʽΪ��y=-
x2+
x+2��
��2����y=-
x2+
x+2��
��y=-
��x-
��2+
��
�������ߵĶԳ�����x=
��
��OD=
��
��C��0��2����
��OC=2��
��Rt��OCD�У��ɹ��ɶ�������
CD=
��
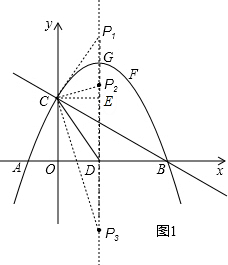
�ߡ�CDP����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3=CD��
��CM��x�Գ�����M��
��MP1=MD=2��
��DP1=4��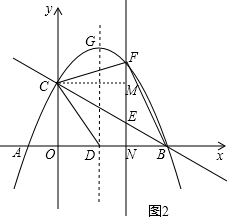
��P1��
��4����P2��
��
����P3��
��-
����
��3����y=0ʱ��0=-
x2+
x+2
��x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��
��
��ã�
��
��ֱ��BC�Ľ���ʽΪ��y=-
x+2��
��ͼ2������C��CM��EF��M����E��a��-
a+2����F��a��-
a2+
a+2����
��EF=-
a2+
a+2-��-
a+2��=-
a2+2a��0��a��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=
BD•OC+
EF•CM+
EF•BN��
=
��
��2+
a��-
a2+2a��+
��4-a����-
a2+2a����
=-a2+4a+
��0��a��4����
=-��a-2��2+
��a=2ʱ��S�ı���CDBF��������=
��
��E��2��1����
 �⣺��1����������y=-
�⣺��1����������y=-| 1 |
| 2 |
��ã�
|
�������ߵĽ���ʽΪ��y=-
| 1 |
| 2 |
| 3 |
| 2 |
��2����y=-
| 1 |
| 2 |
| 3 |
| 2 |
��y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
�������ߵĶԳ�����x=
| 3 |
| 2 |
��OD=
| 3 |
| 2 |
��C��0��2����
��OC=2��
��Rt��OCD�У��ɹ��ɶ�������
CD=
| 5 |
| 2 |
�ߡ�CDP����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3=CD��
��CM��x�Գ�����M��
��MP1=MD=2��
��DP1=4��

��P1��
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
��3����y=0ʱ��0=-
| 1 |
| 2 |
| 3 |
| 2 |
��x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��
|
��ã�
|
��ֱ��BC�Ľ���ʽΪ��y=-
| 1 |
| 2 |
��ͼ2������C��CM��EF��M����E��a��-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��EF=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-a2+4a+
| 5 |
| 2 |
=-��a-2��2+
| 13 |
| 2 |
��a=2ʱ��S�ı���CDBF��������=
| 13 |
| 2 |
��E��2��1����
���������⿼���˴���ϵ������һ�κ����Ľ���ʽ�����ã����κ����Ľ���ʽ�����ã����ɶ��������ã����������ε����ʵ����ã��ı��ε���������ã����ʱ��������Ľ���ʽ�ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ���ڡ�ABC�У�AB=AC��BD=CD��DE��AB��DF��AC������ֱ�Ϊ��E��F��
��ͼ���ڡ�ABC�У�AB=AC��BD=CD��DE��AB��DF��AC������ֱ�Ϊ��E��F�� �ڡ�ABC�У���E��AC�ϣ���
�ڡ�ABC�У���E��AC�ϣ��� ��ͼ���ڡ�ABC�У���ABC=90�㣬D�DZ�AC�ϵ�һ�㣬����BD��ʹ��A=2��1��E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O������D��
��ͼ���ڡ�ABC�У���ABC=90�㣬D�DZ�AC�ϵ�һ�㣬����BD��ʹ��A=2��1��E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O������D��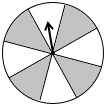 ��һ��������ת����ת����ͼ�����汻�ֳ�8����С����״����ͬ�����Σ���ɫ��Ϊ�ڰ����֣���ָ���λ�ù̶�����ת������ת��������ֹͣ��ָ��ָ���ɫ���εĸ�����
��һ��������ת����ת����ͼ�����汻�ֳ�8����С����״����ͬ�����Σ���ɫ��Ϊ�ڰ����֣���ָ���λ�ù̶�����ת������ת��������ֹͣ��ָ��ָ���ɫ���εĸ�����