题目内容
(1)如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:△ABC≌△CDE.
(2)如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,求OP的长.

(2)如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,求OP的长.

考点:全等三角形的判定,勾股定理,垂径定理
专题:
分析:(1)首先根据平行线的性质可得∠BAC=∠ACE,再加上条件AB=CD,∠B=∠D可利用ASA证明△ABC≌△CDE;
(2)首先过O作OE⊥AB,根据垂径定理可得AE=EB=4cm,再利用勾股定理计算出EO长,再计算出PO长.
(2)首先过O作OE⊥AB,根据垂径定理可得AE=EB=4cm,再利用勾股定理计算出EO长,再计算出PO长.
解答:(1)证明:∵AB∥CE,
∴∠BAC=∠ACE,
在△ABC和△CDE中
,
∴△ABC≌△CDE(ASA);
(2)解: 过O作OE⊥AB,
过O作OE⊥AB,
∵弦AB的长为8cm,
∴AE=EB=4cm,
∵AO=5cm,
∴EO=
=3cm,
∵BE=4cm,BP=2cm,
∴EP=6cm,
∴OP=
=
=3
cm.
∴∠BAC=∠ACE,
在△ABC和△CDE中
|
∴△ABC≌△CDE(ASA);
(2)解:
 过O作OE⊥AB,
过O作OE⊥AB,∵弦AB的长为8cm,
∴AE=EB=4cm,
∵AO=5cm,
∴EO=
| 52-42 |
∵BE=4cm,BP=2cm,
∴EP=6cm,
∴OP=
| EO2+EP2 |
| 9+36 |
| 5 |
点评:此题主要考查了全等三角形的判定,以及垂径定理,关键是掌握证明三角形全等的判定定理.垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
 如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积.
如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积. 如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)
如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)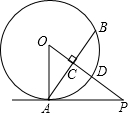 如图:PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4.
如图:PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4. 一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2=
一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2= 如图,△ABC,∠C=90°,CA=CB=11cm,D在AC上,CD=3cm,动点E在CB边上,将线段DE绕D逆时针旋转90°得线段DF,当F恰好落在AB边上时,CE=
如图,△ABC,∠C=90°,CA=CB=11cm,D在AC上,CD=3cm,动点E在CB边上,将线段DE绕D逆时针旋转90°得线段DF,当F恰好落在AB边上时,CE=