Question

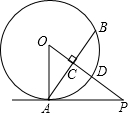如图：PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA=2，OP=4．
（1）求∠POA的度数；
（2）若C为OD中点，连接AD，OB，BD，求证：四边形ADBO是菱形，并求出这个菱形的面积．

Answer 1

考点：切线的性质,菱形的判定与性质

专题：计算题

分析：（1）由PA与圆O相切，得到OA垂直于AP，即三角形AOP为直角三角形，根据OP=2OA，得到∠P=30°，即可求出∠POA的度数；
（2）连接OB，AD，BD，由OP垂直于AB，利用垂径定理得到C为AB中点，再由C为OD中点，得到四边形ADBO为平行四边形，又AB垂直于OD，即可确定出四边形ADBO为菱形，在直角三角形AOC中，由OA长求出OC与AC的长，进而求出OD与AB的长，利用对角线乘积的一半求出菱形ADBO面积即可．

解答：解：（1）∵PA切⊙O于点A，
∴OA⊥AP，即△OAP是Rt△，
∵OA=2，OP=4，即OP=2OA，
∴∠P=30°，
∴∠POA=60°；
（2）连接OB，AD，BD，
∵OP⊥AB，
∴C为AB中点，
∵C为OD中点，
∴四边形ADBO为平行四边形，
∵OD⊥AB，
∴四边形ADBO为菱形；
在Rt△AOC中，∠POA=60°，
∴∠OAC=30°，
∵OA=2，
∴OC=1，根据勾股定理得：AC=

22-12

=

3

，
∴OD=2，AB=2

3

，
则S_菱形ADBO=

1

2

AB•OD=2

3

．

点评：此题考查了切线的性质，勾股定理，直角三角形的性质，以及菱形的判定与性质，熟练掌握切线的性质是解本题的关键．