题目内容
10.如果a-b=2,a-c=-1,那么a2+b2+c2-ab-ac-bc等于7.分析 把多项式扩大二倍,根据完全平方公式写成三个完全平方式,然后根据a-b=2,a-c=-1,求出b-c,代入求解即可.
解答 解:a2+b2+c2-ab-ac-bc
=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2ac-2bc)
=$\frac{1}{2}$[(a2+b2-2ab)+(a2+c2-2ac)+(b2+c2-2bc)]
=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2],
∵a-b=2,a-c=-1,
∴b-c=-3
∴原式=$\frac{1}{2}$(4+1+9)=7.
故答案为:7.
点评 此题考查因式分解的实际运用,完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,解题关键是对原多项式扩大二倍凑成完全平方式.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
18.下列各式中正确的是( )
| A. | 若a>b,则a-1<b-1 | B. | 若a>b,则a2>b2 | ||
| C. | 若a>b,且c≠0,则ac>bc | D. | 若$\frac{a}{|c|}$>$\frac{b}{|c|}$,则a>b |
19.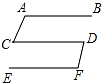 如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
 如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )| A. | 30° | B. | 60° | C. | 150° | D. | 150° |
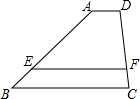 如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.