题目内容
15.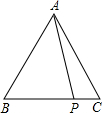 如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值.
如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值.
分析 首先过点A作AD⊥BC于D,可得∠ADP=∠ADB=90°,又由AB=AC,根据三线合一的性质,可得BD=CD,由勾股定理可得PA2=PD2+AD2,AD2+BD2=AB2,然后由AP2+PB•PC=AP2+(BD+PD)(CD-PD),即可求得答案.
解答 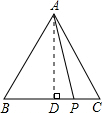 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
∵AB=AC=5,∠ADP=∠ADB=90°,
∴BD=CD,PA2=PD2+AD2,AD2+BD2=AB2,
∴AP2+PB•PC=AP2+(BD+PD)(CD-PD)=AP2+(BD+PD)(BD-PD)=AP2+BD2-PD2=AP2-PD2+BD2=AD2+BD2=AB2=25.
即AP2+PB•BC=25.
点评 本题考查了勾股定理与等腰三角形的性质的正确及灵活运用.注意得到AP2+PB•PC=AP2+(BD+PD)(CD-PD)是解此题的关键.

练习册系列答案
相关题目
5.若线段a,b,c组成直角三角形,则它们的比为( )
| A. | 2:3:4 | B. | 3:4:6 | C. | 4:6:7 | D. | 7:24:25 |
6.两个相似三角形的对应边分别是15cm和25cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
| A. | 75cm,115cm | B. | 60cm,100cm | C. | 85cm,125cm | D. | 45cm,85cm |
3.在下列几张扑克牌中,牌面是中心对称图形的有( )个.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?
道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少? 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=2cm,求⊙O的半径.
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=2cm,求⊙O的半径.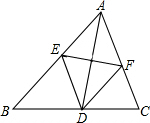 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.