题目内容
10. 道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?
道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?
分析 利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
解答  解:在Rt△AFG中,tan∠AFG=$\frac{AG}{FG}$,
解:在Rt△AFG中,tan∠AFG=$\frac{AG}{FG}$,
∴FG=$\frac{AG}{tan∠AFG}$=$\frac{AG}{\sqrt{3}}$,
在Rt△ACG中,tan∠ACG=$\frac{AG}{CG}$,
∴CG=$\frac{AG}{tan∠ACG}$=$\sqrt{3}$AG.
又∵CG-FG=30m,
即$\sqrt{3}$AG-$\frac{AG}{\sqrt{3}}$=30m,
∴AG=15$\sqrt{3}$m,
∴AB=(15$\sqrt{3}$+2)m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.一元二次方程x2-(x+5)=2(3x-2)的一般形式是( )
| A. | x2-x-5=6x-4 | B. | x2-7x=1 | C. | x2-7x-1=0 | D. | x2-7x-9=0 |
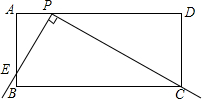 如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E.
如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E. 如图,在矩形ABCD中,E,F为BC上两点,且BE=CF.求证:△ABF≌△DCE.
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF.求证:△ABF≌△DCE.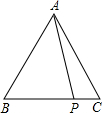 如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值.
如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值.