题目内容
 如图,已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,∠C=∠D.
如图,已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,∠C=∠D.求证:∠A=∠F.
证明:∵∠EQF=∠APB(已知)
∠EQF=∠AQC
∴∠APB=∠AQC(等量代换)
∴BD∥CE
∴∠ABD=∠C
∵∠C=∠D(已知)
∴∠ABD=∠D
∴
∴∠A=∠F
考点:平行线的判定与性质
专题:推理填空题
分析:由条件可先证明BD∥CE,再结合条件可证明DF∥AC,可得∠A=∠F,据此填空即可.
解答:证明:∵∠EQF=∠APB(已知),
∠EQF=∠AQC(对顶角相等),
∴∠APB=∠AQC(等量代换),
∴BD∥CE (同位角相等,两直线平行),
∴∠ABD=∠C(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠ABD=∠D(等量代换),
∴A C∥D F (内错角相等,两直线平行),
∴∠A=∠F (两直线平行,内错角相等).
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;AC;DF;两直线平行,内错角相等.
∠EQF=∠AQC(对顶角相等),
∴∠APB=∠AQC(等量代换),
∴BD∥CE (同位角相等,两直线平行),
∴∠ABD=∠C(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠ABD=∠D(等量代换),
∴A C∥D F (内错角相等,两直线平行),
∴∠A=∠F (两直线平行,内错角相等).
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;AC;DF;两直线平行,内错角相等.
点评:本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
 如图,在宽为30m,长为40m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )
如图,在宽为30m,长为40m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )| A、1200m2 |
| B、1131m2 |
| C、1181 m2 |
| D、1209m2 |
 如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么
如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么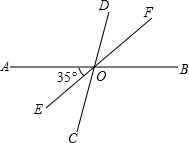 直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF
直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF 如图,在△ABC中,∠C=90°,AD是角平分线,点D到AB的距离为7cm,则CD=
如图,在△ABC中,∠C=90°,AD是角平分线,点D到AB的距离为7cm,则CD=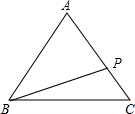 在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是
在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是