题目内容
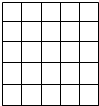 如图:正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.
如图:正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.(1)请在图中画出长度分别为
| 2 |
| 8 |
| 10 |
(2)三角形的三边长分别为
| 2 |
| 8 |
| 10 |
考点:勾股定理
专题:作图题
分析:(1)根据
=
,
=
,
=
画出图形;
(2)根据勾股定理的逆定理进行判断即可.
| 2 |
| 12+12 |
| 8 |
| 22+22 |
| 10 |
| 12+32 |
(2)根据勾股定理的逆定理进行判断即可.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)∵(
)2+(
)2=(
)2,
∴此三角形是直角三角形.
 解:(1)如图所示;
解:(1)如图所示;(2)∵(
| 2 |
| 8 |
| 10 |
∴此三角形是直角三角形.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
化简
÷
•
,其结果是( )
| 16-a2 |
| a2+4a+4 |
| a-4 |
| 2a+4 |
| a+2 |
| a+4 |
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
将抛物线y=x2先向右平移1个单位长度,再向下平移3个单位长度后,所得的抛物线对应的函数关系是( )
| A、y=(x+1)2+3 |
| B、y=(x-1)2-3 |
| C、y=(x+1)2-3 |
| D、y=(x-1)2+3 |
下列说法中正确的是( )
| A、同号两数相乘,积的符号不变 |
| B、异号两数相乘,积取负号 |
| C、互为相反数的两数相乘,积一定为负 |
| D、两个有理数的积的绝对值,不等于这两个有理数的绝对值的积 |
 在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是
在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是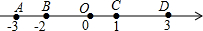 定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题:
定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题: 如图:在Rt△ABC中,∠C=90°,∠B=30°,b=1,则a=
如图:在Rt△ABC中,∠C=90°,∠B=30°,b=1,则a= 如图是4×4正方形网格,其中已有3个小方格涂成了黑色,请你在13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色,请你在13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形.