题目内容
19.函数y=$\frac{k}{x}$的图象经过点(-2,3),则下列各点中在y=$\frac{k}{x}$图象上的是( )| A. | (3,2) | B. | (3,-2) | C. | (-2,-3) | D. | (2,3) |
分析 直接把点A(2,4)代入函数y=kx求出k的值,再把各点代入函数解析式进行检验即可.
解答 解:∵函数y=$\frac{k}{x}$的图象经过点(-2,3),
∴k=-6,
∴反比例函数的解析式为y=-$\frac{6}{x}$,
A、∵当x=3时,y=-2≠2,∴此点不在函数图象上,故A选项错误;
B、∵当x=3时,y=-2,∴此点在函数图象上,故B选项正确;
C、∵当x=-2时,y=3≠-3,∴此点不在函数图象上,故C选项错误;
D、∵当x=2时,y=-3≠3,∴此点不在函数图象上,故D选项错误.
故选:B.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.若n边形的所有内角与某一个外角的总和为1297°,则n等于( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
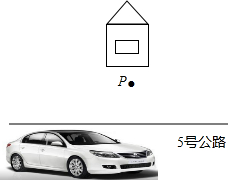 如图所示,一次缉毒行动中,警方获可靠信息,一运毒车将经过5号公路,但由于车上有爆炸装置,警方无法靠近,只能使用远程射击的方法,为了减少对周围的伤亡,警方选中一距离公路120m的隐蔽处P点,射程为200m,准备行动,此时发现,运毒车已经来到与P点的水平距离为300m处,若运毒车的车速为20m/s,那警察发现后要在几秒钟内对其进行射击?
如图所示,一次缉毒行动中,警方获可靠信息,一运毒车将经过5号公路,但由于车上有爆炸装置,警方无法靠近,只能使用远程射击的方法,为了减少对周围的伤亡,警方选中一距离公路120m的隐蔽处P点,射程为200m,准备行动,此时发现,运毒车已经来到与P点的水平距离为300m处,若运毒车的车速为20m/s,那警察发现后要在几秒钟内对其进行射击?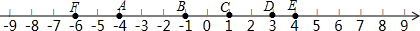
 如图,已知∠2是△ABC的一个外角.求证:∠2=∠A+∠B.
如图,已知∠2是△ABC的一个外角.求证:∠2=∠A+∠B.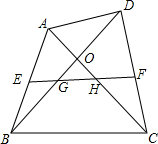 如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.
如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.