题目内容
9.已知抛物线经过点P(-2,0)和Q(8,0),顶点在直线y=$\frac{25}{3}$上,则该抛物线的解析式为y=-$\frac{1}{3}$(x-3)2+$\frac{25}{3}$.分析 根据已知条件求得顶点坐标为(3,$\frac{25}{3}$),设出顶点式,把P的坐标代入即可求得.
解答 解:∵抛物线经过点P(-2,0)和Q(8,0),
∴对称轴x=$\frac{-2+8}{2}$=3,
∵顶点在直线y=$\frac{25}{3}$上,
∴抛物线的顶点坐标为(3,$\frac{25}{3}$),
设抛物线的解析式为y=a(x-3)2+$\frac{25}{3}$,
把P(-2,0)代入得a(-2-3)2+$\frac{25}{3}$=0,
解得a=-$\frac{1}{3}$,
∴该抛物线的解析式为y=-$\frac{1}{3}$(x-3)2+$\frac{25}{3}$.
故答案为y=-$\frac{1}{3}$(x-3)2+$\frac{25}{3}$.
点评 本题考查了待定系数法求函数解析式,解题的关键是求得顶点坐标.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
19.函数y=$\frac{k}{x}$的图象经过点(-2,3),则下列各点中在y=$\frac{k}{x}$图象上的是( )
| A. | (3,2) | B. | (3,-2) | C. | (-2,-3) | D. | (2,3) |
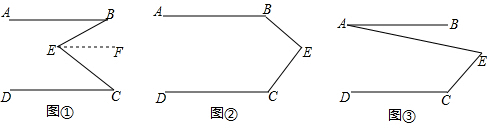
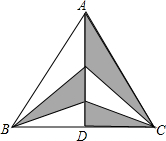 如图,△ABC中,AD是BC的中垂线,若BC=8,AD=6,则图中阴影部分的面积是12.
如图,△ABC中,AD是BC的中垂线,若BC=8,AD=6,则图中阴影部分的面积是12. 如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?
如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?