题目内容
9．若n边形的所有内角与某一个外角的总和为1297°，则n等于（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
分析 根据n边形的内角和定理可知：n边形内角和为（n-2）×180．设这个外角度数为x度，利用方程和不等式即可求出答案．
解答 解：设这个外角度数为x°，根据题意，得
（n-2）×180+x=1297，
180n-360+x=1297，
x=1297+360-180n，即x=1657-180n，
由于0＜x＜180，即0＜1657-180n＜180，
解得，8$\frac{37}{180}$＜n＜9$\frac{37}{180}$，
则n=9．
故选：D．
点评 本题考查的是多边形内角的计算，掌握n边形内角和为（n-2）×180是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
19．函数y=$\frac{k}{x}$的图象经过点（-2，3），则下列各点中在y=$\frac{k}{x}$图象上的是（ ）
| A． | （3，2） | B． | （3，-2） | C． | （-2，-3） | D． | （2，3） |
如图所示是边长为1的正方形网格，点A、B、C、D都在格点上．求图中阴影部分的面积．
由几个小立方块搭成的几何体从正面和左面看到的图形相同．如图，请你判断一下，最多有多少个小正方体？最少有多少个小正方体？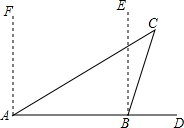
如图，一艘轮船上午8时在A处沿正东方向行驶，在A处测得灯塔C在北偏东60°方向上，行驶1小时后到达B处，在B处测得灯塔C在北偏东20°方向上．求△ABC各内角及∠DBC的度数．
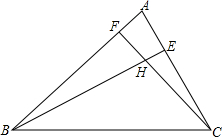在△ABC中，已知∠ABC=45°，∠ACB=60°，BE是AC上的高，CF交AB于点F，交BE于点H，且∠BHC=105°，△BFH是直角三角形吗？为什么？