题目内容
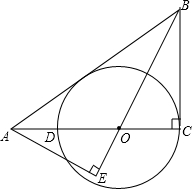 如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.
如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.(1)求证:AB是⊙O的切线;
(2)若BC=6,tan∠BAC=
| 3 |
| 4 |
考点:切线的判定
专题:证明题
分析:(1)作OH⊥AB于H,由AE2=OE•BE,∠AEO=∠BEA可判断△EAO∽△EBA,得到∠1=∠2,再证明∠1=∠3,则∠2=∠3,根据角平分线性质得OC=OH,然后根据切线的判定定理得到AB是⊙O的切线;
(2)在Rt△ABC中,根据正切的定义可计算出AC=8,再根据勾股定理计算出AB=10,然后根据切线长定理得BC=BH=6,则AH=AB-BH=4;Rt△AHO中,根据正切的定义计算出OH=3,则OC=3,所以AO=5,利用勾股定理计算出OB=3
,再证明Rt△OAE∽Rt△OBC,利用相似比可计算出AE.
(2)在Rt△ABC中,根据正切的定义可计算出AC=8,再根据勾股定理计算出AB=10,然后根据切线长定理得BC=BH=6,则AH=AB-BH=4;Rt△AHO中,根据正切的定义计算出OH=3,则OC=3,所以AO=5,利用勾股定理计算出OB=3
| 5 |
解答:(1)证明:作OH⊥AB于H,如图,
∵AE2=OE•BE,
∴AE:OE=BE:AE,
而∠AEO=∠BEA,
∴△EAO∽△EBA,
∴∠1=∠2,
∵∠4=∠5,
∴∠1=∠3,
∴∠2=∠3,即OB为∠ABC的平分线,
∴OC=OH,
∴AB是⊙O的切线;
(2)解:在Rt△ABC中,tan∠BAC=
=
,
而BC=6,
∴AC=8,
∴AB=
=10,
∵BH和BC都是⊙O的切线,
∴BC=BH=6,
∴AH=AB-BH=4,
在Rt△AHO中,tan∠HAO=
=
,
∴OH=3,
∴OC=3,
∴AO=AC-OC=5,
在△OBC中,OB=
=
=3
,
∵∠1=∠3,
∴Rt△OAE∽Rt△OBC,
∴
=
,即
=
,
∴AE=2
.
∵AE2=OE•BE,
∴AE:OE=BE:AE,
而∠AEO=∠BEA,

∴△EAO∽△EBA,
∴∠1=∠2,
∵∠4=∠5,
∴∠1=∠3,
∴∠2=∠3,即OB为∠ABC的平分线,
∴OC=OH,
∴AB是⊙O的切线;
(2)解:在Rt△ABC中,tan∠BAC=
| BC |
| AC |
| 3 |
| 4 |
而BC=6,
∴AC=8,
∴AB=
| AC2+BC2 |
∵BH和BC都是⊙O的切线,
∴BC=BH=6,
∴AH=AB-BH=4,
在Rt△AHO中,tan∠HAO=
| OH |
| AH |
| 3 |
| 4 |
∴OH=3,
∴OC=3,
∴AO=AC-OC=5,
在△OBC中,OB=
| BC2+OC2 |
| 62+32 |
| 5 |
∵∠1=∠3,
∴Rt△OAE∽Rt△OBC,
∴
| AE |
| BC |
| OA |
| OB |
| AE |
| 6 |
| 5 | ||
3
|
∴AE=2
| 5 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
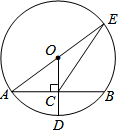 如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
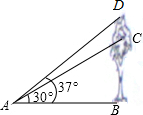 九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)
九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)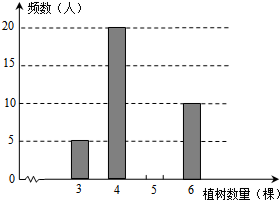 今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).