��Ŀ����
�Ķ��������ϣ�
С����������һ�����⣺��ͼ1�������Ϊa�ġ�ABC��ν������²������ֱ��ӳ�AB��BC��CA��A1��B1��C1��ʹ��A1B=AB��B1C=BC��C1A=CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS1����S1��ֵ��
С��������˼���ͽ���������ģ���ͼ2������A1C��B1A��C1B����ΪA1B=AB��B1C=BC��C1A=CA�����ݵȸ��������ε�����ȵ��ڵ�֮�ȣ�����S ��A1BC=S ��B1CA=S ��C1AB=S��ABC=a���ɴ˼����������Ӷ������������⣮
��1����ֱ��д��S1= �����ú���ĸa��ʽ�ӱ�ʾ����
��ο�С��ͬѧ˼������ķ���������������⣺
��2����ͼ3�������Ϊa�ġ�ABC��ν������²������ֱ��ӳ�AB��BC��CA��A1��B1��C1��ʹ��A1B=2AB��B1C=2BC��C1A=2CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS2����S2��ֵ��
��3����ͼ4��PΪ��ABC��һ�㣬����AP��BP��CP���ӳ��ֱ�BC��AC��AB�ڵ�D��E��F����ѡ�ABC�ֳ�����С�����Σ������ĸ�С�������������ͼ�ϱ��������APE�����Ϊy����BPF�����Ϊx�������APE����BPF����APF���֮��Ĺ�ϵ�������ABC�������
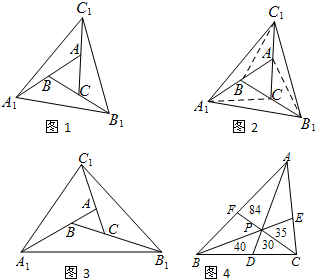
С����������һ�����⣺��ͼ1�������Ϊa�ġ�ABC��ν������²������ֱ��ӳ�AB��BC��CA��A1��B1��C1��ʹ��A1B=AB��B1C=BC��C1A=CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS1����S1��ֵ��
С��������˼���ͽ���������ģ���ͼ2������A1C��B1A��C1B����ΪA1B=AB��B1C=BC��C1A=CA�����ݵȸ��������ε�����ȵ��ڵ�֮�ȣ�����S ��A1BC=S ��B1CA=S ��C1AB=S��ABC=a���ɴ˼����������Ӷ������������⣮
��1����ֱ��д��S1=
��ο�С��ͬѧ˼������ķ���������������⣺
��2����ͼ3�������Ϊa�ġ�ABC��ν������²������ֱ��ӳ�AB��BC��CA��A1��B1��C1��ʹ��A1B=2AB��B1C=2BC��C1A=2CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS2����S2��ֵ��
��3����ͼ4��PΪ��ABC��һ�㣬����AP��BP��CP���ӳ��ֱ�BC��AC��AB�ڵ�D��E��F����ѡ�ABC�ֳ�����С�����Σ������ĸ�С�������������ͼ�ϱ��������APE�����Ϊy����BPF�����Ϊx�������APE����BPF����APF���֮��Ĺ�ϵ�������ABC�������

���㣺������Ȼ��任
ר�⣺
��������1������������ͬ�ߵȵ������ȣ�����������ɣ�
��2������������ͬ�߲��ȵ������Ϊ�ױ߳��ıȣ�����������ɣ�
��3�����������������֮���ϵ�ó���߳��ȣ������ó���APE����BPF����APF���֮��Ĺ�ϵ��
����
=
=
��
=
=
�ó�����x��y�ķ���������ɣ�
��2������������ͬ�߲��ȵ������Ϊ�ױ߳��ıȣ�����������ɣ�
��3�����������������֮���ϵ�ó���߳��ȣ������ó���APE����BPF����APF���֮��Ĺ�ϵ��
����
| S��APB |
| S��BPD |
| AP |
| PD |
| x+84 |
| 40 |
| S��APC |
| S��PCD |
| AP |
| PD |
| y+35 |
| 30 |
����⣺��1����B1C=BC��A1B=AB��
��S��ABC=S��BCA1��S��BCA1=S��A1CB1��
��S��A1B1C=2S��ABC=2a��
ͬ���ɵó���S��A1AC1=S��CB1C1=2a��
��S1=2a+2a+2a+a=7a��
�ʴ�Ϊ��7a��
��2����A1B=2AB��B1C=2BC��C1A=2CA
���ݵȸ��������ε�����ȵ��ڵ�֮�ȣ�
��S��A1BC=S��B1CA=S��C1AB=2S��ABC=2a��
��S��A1B1C=2S��A1BC=4a��
��S��A1B1B=6S��ABC=6a��
ͬ���ɵó���S��A1AC1=S��CB1C1=6a��
��S2=19a��
��3���ٹ���C��CG��BE�ڵ�G��
��S��BPC=
BP•CG=70��S��PCE=
PE•CG=35��
��
=
=
=2
��
=2������BP=2EP
ͬ����
=
=2
��S��APB=2S��APF=x��S��APE=y��
��x+84=2y��
��S��APB+84=2S��APE��2S��APF+84=2S��APE��
�ڡ�
=
=
��
=
=
��
=
��
�֡�x+84=2y
��
��
��S��BPF=56��S��APE=70��
��S��ABC=40+30+35+84+56+70=315��
��S��ABC=S��BCA1��S��BCA1=S��A1CB1��
��S��A1B1C=2S��ABC=2a��
ͬ���ɵó���S��A1AC1=S��CB1C1=2a��
��S1=2a+2a+2a+a=7a��
�ʴ�Ϊ��7a��
��2����A1B=2AB��B1C=2BC��C1A=2CA

���ݵȸ��������ε�����ȵ��ڵ�֮�ȣ�
��S��A1BC=S��B1CA=S��C1AB=2S��ABC=2a��
��S��A1B1C=2S��A1BC=4a��
��S��A1B1B=6S��ABC=6a��
ͬ���ɵó���S��A1AC1=S��CB1C1=6a��
��S2=19a��
��3���ٹ���C��CG��BE�ڵ�G��
��S��BPC=
| 1 |
| 2 |
| 1 |
| 2 |
��
| S��BPC |
| S��PCE |
| BP•CG |
| PE•CG |
| 70 |
| 35 |
��
| BP |
| EP |
ͬ����
| S��APB |
| S��APE |
| BP |
| PE |
��S��APB=2S��APF=x��S��APE=y��
��x+84=2y��
��S��APB+84=2S��APE��2S��APF+84=2S��APE��
�ڡ�
| S��APB |
| S��BPD |
| AP |
| PD |
| x+84 |
| 40 |
| S��APC |
| S��PCD |
| AP |
| PD |
| y+35 |
| 30 |
��
| x+84 |
| 40 |
| y+35 |
| 30 |
�֡�x+84=2y
��
|
��S��BPF=56��S��APE=70��
��S��ABC=40+30+35+84+56+70=315��
������������Ҫ������������Ȼ��任������������ͬ�����������ױ߹�ϵ�ֱ�����ó��ǽ���ؼ���

��ϰ��ϵ�д�
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
�����Ŀ
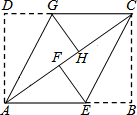 ��ͼ��ABCD�Ǿ���ֽƬ�����ۡ�B����D��ʹBC��ADǡ������AC�ϣ�����F��H�ֱ���B��D����㣮��֤���ı���AECG��ƽ���ı��Σ�
��ͼ��ABCD�Ǿ���ֽƬ�����ۡ�B����D��ʹBC��ADǡ������AC�ϣ�����F��H�ֱ���B��D����㣮��֤���ı���AECG��ƽ���ı��Σ�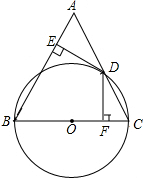 ��ͼ����ABC�У�AB=BC����BCΪֱ���ġ�O��AC�ڵ�D������D��DE��AB��DF��BC������ֱ�ΪE��F��
��ͼ����ABC�У�AB=BC����BCΪֱ���ġ�O��AC�ڵ�D������D��DE��AB��DF��BC������ֱ�ΪE��F�� ��ͼ����?ABCD�У���E����F�ֱ���AD��CB���ӳ����ϣ���DE=BF������EF�ֱ�AB��CD�ڵ�H����G��
��ͼ����?ABCD�У���E����F�ֱ���AD��CB���ӳ����ϣ���DE=BF������EF�ֱ�AB��CD�ڵ�H����G��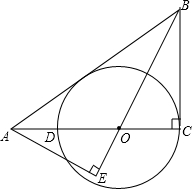 ��ͼ����ABC�У���C=90�㣬O����AC���ϣ���OΪԲ�ģ�OCΪ�뾶��Բ��AC����һ������ΪD��AE��BO���ӳ�����E�㣬��AE2=OE•BE��
��ͼ����ABC�У���C=90�㣬O����AC���ϣ���OΪԲ�ģ�OCΪ�뾶��Բ��AC����һ������ΪD��AE��BO���ӳ�����E�㣬��AE2=OE•BE�� ��ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
��ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
 ����������y=
����������y=