题目内容
 如图,已知矩形OABC的面积为81,它的对角线OB与双曲线y=
如图,已知矩形OABC的面积为81,它的对角线OB与双曲线y=| k |
| x |
考点:反比例函数综合题
专题:
分析:过D点作DE⊥OA,设D(m,-n),则OE=m,DE=n,DE∥AB,利用相似三角形对应边成比例,求OA与OB的积,再利用矩形面积公式,列方程求k的值.
解答:解:如图,过D点作DE⊥OA,垂足为E,
设D(m,-n),则OE=m,DE=n,
∵四边形OABC为矩形,∴DE∥AB,
∴△ODE∽△OBA,∴
=
=
=
,
∴OA=
m,AB=
n,
∵矩形OABC的面积为81,∴OA•OB=81,即
m×
n=81,
解得mn=25,
∴k=-mn=-25,
故答案为:-25.

设D(m,-n),则OE=m,DE=n,
∵四边形OABC为矩形,∴DE∥AB,
∴△ODE∽△OBA,∴
| OE |
| OA |
| DE |
| AB |
| OD |
| OB |
| 5 |
| 5+4 |
∴OA=
| 9 |
| 5 |
| 9 |
| 5 |
∵矩形OABC的面积为81,∴OA•OB=81,即
| 9 |
| 5 |
| 9 |
| 5 |
解得mn=25,
∴k=-mn=-25,
故答案为:-25.

点评:本题考查了反比例函数的综合运用.关键是设D点坐标,表示线段长度,利用相似三角形表示矩形两邻边的积,根据矩形面积公式求两邻边的积.

练习册系列答案
相关题目
在打靶中,某运动员每发子弹都是命中8、9、10环,他打了多于11发子弹,共得100环,那么,他命中10环的次数是( )
| A、0 | B、1 | C、2 | D、不能确定 |
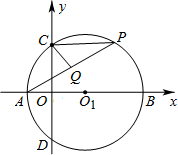 如图,在直角坐标系中,O1(3,0),A(-2,0),以O1为圆心,O1A为半径的⊙O1交y轴于C、D两点,P为弧BC上一点,CQ平分∠DCP,交AP于点Q,则AQ的长为( )
如图,在直角坐标系中,O1(3,0),A(-2,0),以O1为圆心,O1A为半径的⊙O1交y轴于C、D两点,P为弧BC上一点,CQ平分∠DCP,交AP于点Q,则AQ的长为( )A、2
| ||
| B、4 | ||
| C、5 | ||
D、3
|
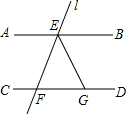 如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )
如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )| A、115° | B、125° |
| C、130° | D、100° |
 已知△ABC三边的长分别为5、12、13,那么△ABC内切圆的半径为
已知△ABC三边的长分别为5、12、13,那么△ABC内切圆的半径为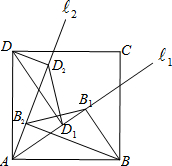 如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由.
如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由. 甲在B地,乙在A地,甲步行,乙骑自行车,他们同时去C地(A、B、C在同一条直线上),下面图象表示他们距A地的路程S(千米)与时间t(小时)之间的函数关系式.结合图象回答下列问题:
甲在B地,乙在A地,甲步行,乙骑自行车,他们同时去C地(A、B、C在同一条直线上),下面图象表示他们距A地的路程S(千米)与时间t(小时)之间的函数关系式.结合图象回答下列问题: 如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=
如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=