题目内容
9.计算:(1)$\frac{{{m^2}-4m}}{{16-{m^2}}}$
(2)$\frac{a}{a-1}÷\frac{{{a^2}-a}}{{{a^2}-1}}-\frac{1}{a+1}$
(3)$\frac{1}{{{a^2}-{b^2}}}÷(\frac{1}{a+b}-\frac{1}{a-b})$.
分析 (1)先因式分解,再约分即可;
(2)先因式分解,再约分,再通分,根据分式的除法和减法法则进行计算即可;
(3)先算括号里面的,再因式分解,约分即可.
解答 解:(1)原式=$\frac{m(m-4)}{(4+m)(4-m)}$
=-$\frac{m}{m+4}$;
(2)原式=$\frac{a}{a-1}$•$\frac{(a+1)(a-1)}{a(a-1)}$-$\frac{1}{a+1}$
=$\frac{a+1}{a-1}$-$\frac{1}{a+1}$
=$\frac{(a+1)^{2}}{(a+1)(a-1)}$-$\frac{a-1}{(a+1)(a-1)}$
=$\frac{{a}^{2}+2a+1-a+1}{{a}^{2}-1}$
=$\frac{{a}^{2}+a+2}{{a}^{2}-1}$;
(3)原式=$\frac{1}{(a+1)(a-1)}$÷($\frac{a-b}{(a+b)(a-b)}$-$\frac{a+b}{(a+b)(a-b)}$)
=$\frac{1}{(a+1)(a-1)}$•$\frac{(a+b)(a-b)}{a-b-a-b}$
=$\frac{{a}^{2}-{b}^{2}}{-2{a}^{2}b+2b}$.
点评 本题考查了分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.某商场用2300元购进A、B两种新型节能台灯共40盏,这两种台灯的进价、标价如下表所示.
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
| 类型 价格 | A型 | B型 |
| 进价(元/盏) | 35 | 65 |
| 标价(元/盏) | 50 | 100 |
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
17.小明在解关于x的方程5a+x=10时,误将“+x”看作“-x”,得方程的解为x=3,则原方程的解为( )
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
4.如果x2+4x+k2恰好是另一个整式的平方,那么常数k的值为( )
| A. | 4 | B. | 2 | C. | -2 | D. | ±2 |
14.抛物线y=-5(x-2)2+3的顶点坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
19.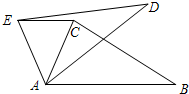 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
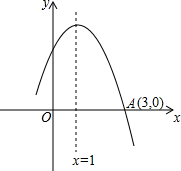 如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( )
如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( )