题目内容
12.已知$A=(x-3)÷\frac{{(x+2)({x^2}-6x+9)}}{{{x^2}-4}}-1$(1)化简A;
(2)若x满足不等式组$\left\{\begin{array}{l}2x-1<x\\ 1-\frac{x}{3}<\frac{4}{3}\end{array}\right.$,且x为整数时,求A的值.
分析 (1)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,确定出整数x的值,代入计算即可求出A的值.
解答 解:(1)A=(x-3)•$\frac{(x+2)(x-2)}{(x+2)(x-3)^{2}}$-1=$\frac{x-2}{x-3}$-1=$\frac{x-2-x+3}{x-3}$=$\frac{1}{x-3}$;
(2)$\left\{\begin{array}{l}{2x-1<x①}\\{1-\frac{x}{3}<\frac{4}{3}②}\end{array}\right.$,
由①得:x<1,
由②得:x>-1,
∴不等式组的解集为-1<x<1,即整数x=0,
则A=-$\frac{1}{3}$.
点评 此题考查了分式的混合运算,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.在下列二次根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
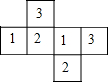 一个质地均匀的正方体的每个面上都标有数字1,2,3中的一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的面上数字相同的概率是$\frac{1}{3}$.
一个质地均匀的正方体的每个面上都标有数字1,2,3中的一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的面上数字相同的概率是$\frac{1}{3}$.
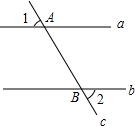 如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=60°.
如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=60°.