题目内容
7．已知$\sqrt{36-{a}^{2}}$-$\sqrt{4-{a}^{2}}$=4，则$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$的值是（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 把$\sqrt{36-{a}^{2}}$-$\sqrt{4-{a}^{2}}$=4两边同乘$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$，进一步整理得出答案即可．
解答 解：∵$\sqrt{36-{a}^{2}}$-$\sqrt{4-{a}^{2}}$=4，
∴（$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$）（$\sqrt{36-{a}^{2}}$-$\sqrt{4-{a}^{2}}$）=4（$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$），
即4（$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$）=32，
∴$\sqrt{36-{a}^{2}}$+$\sqrt{4-{a}^{2}}$=8．
故选：D．
点评 此题考查二次根式的化简求值，利用平方差公式化简是解决问题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图，△ABC≌△FED，∠ABM=∠FEN，点A、M、D、C、N、F在同一条直线上，那么BM与EN平行吗？请说明理由．
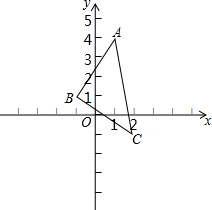如图，写出△ABC中各顶点坐标，在同一坐标系中画出直线m：x=-1．并作出△ABC关于直线m对称的△A′B′C′．若P（a，b）是AC边上一点．请表示其在△A′B′C′中对应点的坐标．
如图，某学校教学楼前有一个边长为40m的正方形广场，学校准备在其中心建一个半径为10m的圆形花坛，在四个角落处分别建一个正方形花坛，每个小正方形花坛完全一样，其余部分铺设地砖，要求铺设地砖的区域占总面积的$\frac{9}{16}$．（π取3）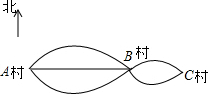
如图，从A村去B村有3条道路，从B村去C村有2条道路．