题目内容
14．能确定四边形是平行四边形的条件的是（ ）| A． | 一组对边平行，另一组对边相等 | B． | 一组对边平行，一组邻角相等 | ||
| C． | 一组对边平行且相等 | D． | 两条对角线相等 |
分析 由平行四边形的判定方法和梯形的判定方法容易得出结论．
解答 解：A、一组对边平行，另一组对边相等的四边形是梯形，不一定是平行四边形，选项A错误；
B、一组对边平行，一组邻角相等的四边形可能是梯形，不一定是平行四边形，选项B错误；
C、一组对边平行且相等的四边形是平行四边形，选项C正确；
D、两条对角线相等的四边形不一定是平行四边形，选项D错误；
故选：C．
点评 本题考查了平行四边形的判定方法、梯形的判定方法；熟记平行四边形的判定方法是解决问题的关键．
练习册系列答案
相关题目
5．方程$\frac{2}{x}=\frac{3}{x-1}$的解为（ ）
| A． | x=-2 | B． | x=2 | C． | x=-1 | D． | x=$\frac{1}{2}$ |
2．
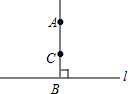如图所示，因为AB⊥l，BC⊥l，B为垂足，所以AB和BC重合，其理由是（ ）
如图所示，因为AB⊥l，BC⊥l，B为垂足，所以AB和BC重合，其理由是（ ）| A． | 两点确定一条直线 | |
| B． | 在同一平面内，过一点有且只有一条直线与已知直线垂直 | |
| C． | 过一点能作一条垂线 | |
| D． | 垂线段最短 |
如图，在四边形ABCD中，AD∥BC，AD=8，BC=16，点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动，点P停止运动时，点Q也随之停止运动，设运动时间为t秒．
3．计算-$\frac{1}{2}$-1的结果等于（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | $-\frac{3}{2}$ |
4．
如图是一个正方体的表面展开图，则原正方体标有数字“1”所在面的对面标有数字（ ）
如图是一个正方体的表面展开图，则原正方体标有数字“1”所在面的对面标有数字（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |