题目内容
已知y与x成一次函数,当x=1时,y=3,当x=2时,y=7.
(1)求出y与x之间的函数关系式;
(2)说明:点P(-1,-3)在这个一次函数的图象上;
(3)如果这个一次函数的图象经过点(m,2),求m.
(1)求出y与x之间的函数关系式;
(2)说明:点P(-1,-3)在这个一次函数的图象上;
(3)如果这个一次函数的图象经过点(m,2),求m.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)设y与x的关系式为y=kx+b(k≠0),利用待定系数法求函数解析式解答即可;
(2)把x=-1代入函数关系式计算即可判断;
(3)把点的坐标代入函数关系式计算即可得解.
(2)把x=-1代入函数关系式计算即可判断;
(3)把点的坐标代入函数关系式计算即可得解.
解答:解:(1)设y与x的关系式为y=kx+b(k≠0),
则
,
解得
,
所以,y与x之间的函数关系式为y=4x-1;
(2)当x=-1时,y=4×(-1)-1=-5≠-3,
所以,点P(-1,-3)不在这个一次函数的图象上;
(3)∵这个一次函数的图象经过点(m,2),
∴4m-1=2,
解得m=
.
则
|
解得
|
所以,y与x之间的函数关系式为y=4x-1;
(2)当x=-1时,y=4×(-1)-1=-5≠-3,
所以,点P(-1,-3)不在这个一次函数的图象上;
(3)∵这个一次函数的图象经过点(m,2),
∴4m-1=2,
解得m=
| 3 |
| 4 |
点评:本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,待定系数法是求函数解析式常用的方法,需熟练掌握.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,∠BAC=100°,MN、EF分别垂直平分AB、AC,则∠MAE的大小为( )
如图,∠BAC=100°,MN、EF分别垂直平分AB、AC,则∠MAE的大小为( )| A、80° | B、20° |
| C、50° | D、10° |
若2:3=7:x,则x=( )
| A、2 | B、3 | C、3.5 | D、10.5 |
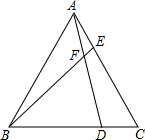 如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F. 如图,在大圆中有一小圆O,作直线l,使其将两圆的面积均二等分.
如图,在大圆中有一小圆O,作直线l,使其将两圆的面积均二等分.