题目内容
20.已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC,CB于点E,F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断$\frac{1}{DM}+\frac{1}{DN}$是否为定值?若是,请求出该定值;若不是,请说明理由.
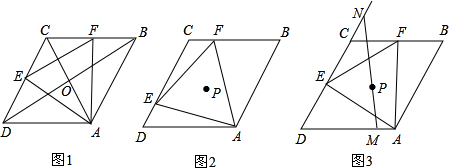
分析 (1)首先分别连接OE、0F,由四边形ABCD是菱形,即可得AC⊥BD,BD平分∠ADC.AD=DC=BC,又由E、F分别为DC、CB中点,即可证得0E=OF=OA,则可得点O即为△AEF的外心;
(2)①首先分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,即可求得∠IPJ的度数,又由点P是等边△AEF的外心,易证得△PIE≌△PJA,可得PI=PJ,即点P在∠ADC的平分线上,即点P落在直线DB上.
②当AE⊥DC时.△AEF面积最小,此时点E、F分别为DC、CB中点.连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.由△GBP∽△MDP,即可$\frac{1}{DM}+\frac{1}{DN}$为定值2.
解答 (1)证明:如图①,分别连接OE、0F,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ADC.AD=DC=BC,
∴∠COD=∠COB=∠AOD=90°.
∠ADO=$\frac{1}{2}$∠ADC=$\frac{1}{2}$×60°=30°,
又∵E、F分别为DC、CB中点,
∴OE=$\frac{1}{2}$CD,OF=$\frac{1}{2}$BC,AO=$\frac{1}{2}$AD,
∴0E=OF=OA,
∴点O即为△AEF的外心;
(2)解:①猜想:外心P一定落在直线DB上.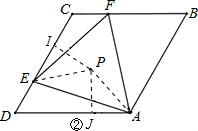 证明:如图②,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,
证明:如图②,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,
∴∠PIE=∠PJD=90°,
∵∠ADC=60°,
∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120°,
∵点P是等边△AEF的外心,
∴∠EPA=120°,PE=PA,
∴∠IPJ=∠EPA,
∴∠IPE=∠JPA,
∴△PIE≌△PJA,
∴PI=PJ,
∴点P在∠ADC的平分线上,即点P落在直线DB上;
②$\frac{1}{DM}+\frac{1}{DN}$为定值2,
当AE⊥DC时.△AEF面积最小,
此时点E、F分别为DC、CB中点.
连接BD、AC交于点P,由(1)
可得点P在BD上,即为△AEF的外心,
如图③.设MN交BC于点G,
设DM=x,DN=y(x≠0.y≠O),则CN=y-1,
∵BC∥DA,
∴△GBP≌△MDP,
∴BG=DM=x,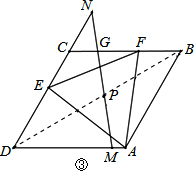
∴CG=1-x,
∵BC∥DA,
∴△NCG∽△NDM,
∴$\frac{CN}{DN}=\frac{CG}{DM}$,
∴$\frac{y-1}{y}$=$\frac{1-x}{x}$,
∴x+y=2xy,
∴$\frac{1}{x}$+$\frac{1}{y}$=2,
即$\frac{1}{DM}+\frac{1}{DN}$=2.
点评 此题考查了相似三角形的判定与性质,三角形的外心的判定与性质,以及菱形的性质等知识.此题综合性很强,图形也比较复杂,解题的关键是方程思想与数形结合思想的应用.

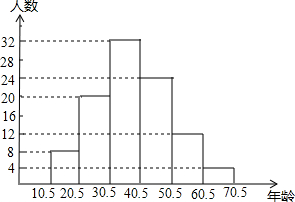 今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
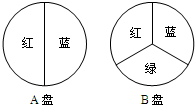 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.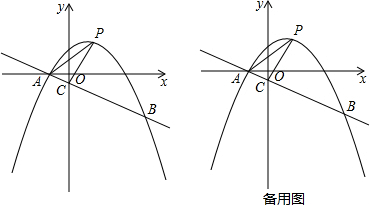
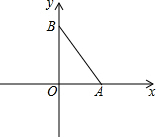 如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).
如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).