题目内容
13.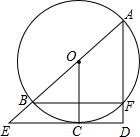 如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$.
如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$.
分析 连接AC,根据切线的性质得OC⊥DE,而AD⊥EC,则OC∥AD,理由平行线的性质得∠OCA=∠DAC,加上∠OCA=∠OAC,所以∠OAC=∠DAC,即可得到结论.
解答  证明:连接AC,
证明:连接AC,
∵DE切⊙O于C,
∴OC⊥DE,
∵AD⊥EC,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴OC平分$\widehat{BF}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理、等腰三角形的判定与性质,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3.下列说法正确的是( )
| A. | 任何有理数都有倒数 | |
| B. | 一个数的倒数-定小于这个数 | |
| C. | 倒数等于它本身的数有±1和0 | |
| D. | 一个有理数的倒数的符号与它本身的符号相同 |
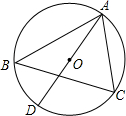 如图,△ABC是⊙O内接三角形,AD是⊙O的直径,AD=6,∠ABC=∠CAD,求弦AC所对的弧长.
如图,△ABC是⊙O内接三角形,AD是⊙O的直径,AD=6,∠ABC=∠CAD,求弦AC所对的弧长. 某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,
某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,