题目内容
8. 某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,
某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,(1)冬至正午时住宅楼的影子落在教学楼上有多高?(精确到 0.1m)
(2)要使冬至正午的太阳能够照到教学楼的墙角.则两楼间的距离至少应为多少?(精确到0.1m)
分析 (1)作DE⊥AC于E,根据正切的概念和题意列出关系式,解答即可;
(2)根据正切的概念进行计算即可.
解答 解:(1)如图住宅楼为甲,教学楼为乙,
作DE⊥AC于E,
由题意可知∠ADE=30°,DE=BC=19.2m,
∵在Rt△ADE中,∠AED=90°,∠ADE=30°,
∴tan∠ADE=$\frac{AE}{DE}$,
则AE=19.2×$\frac{\sqrt{3}}{3}$≈11.1,
∴DB=15.6-11.1=4.5m;
(2)∵tan∠ADE=$\frac{AE}{DE}$,
当AE=15.6时,正午的太阳能够照到教学楼的墙角,
∴DE≈27m.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念、正确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
17. 如图是日本三菱汽车公司的标志,该图形绕点O按下列角度旋转,能与自身重合的是( )
如图是日本三菱汽车公司的标志,该图形绕点O按下列角度旋转,能与自身重合的是( )
 如图是日本三菱汽车公司的标志,该图形绕点O按下列角度旋转,能与自身重合的是( )
如图是日本三菱汽车公司的标志,该图形绕点O按下列角度旋转,能与自身重合的是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
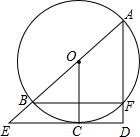 如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$.
如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$.