题目内容
1.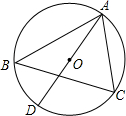 如图,△ABC是⊙O内接三角形,AD是⊙O的直径,AD=6,∠ABC=∠CAD,求弦AC所对的弧长.
如图,△ABC是⊙O内接三角形,AD是⊙O的直径,AD=6,∠ABC=∠CAD,求弦AC所对的弧长.
分析 连接CD、OC根据弧、弦、圆周角之间的关系证明△ACD是等腰直角三角形,即可求得AC的长,利用弧长公式即可求得弧AC的长.
解答 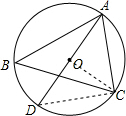 解:连接CD、OC.
解:连接CD、OC.
∵∠ABC=∠CAD,
∴$\widehat{AC}$=$\widehat{CD}$,
∴AC=CD,
又∵AD是⊙O的直径,
∴∠ACD=90°,
∴△ACD是等腰直角三角形,
∴AC=CD=$\frac{\sqrt{2}}{2}$×AD=3$\sqrt{2}$,
∠AOC=90°,
则劣弧AC的长是$\frac{90π×3}{180}$=$\frac{3π}{2}$.优弧AC=$\frac{9}{2}π$
点评 本题考查了弧长的计算公式以及圆周角、弧、弦之间的关系,证明△ACD是等腰直角三角形是关键.

练习册系列答案
相关题目
9.若3x2-3x+2-x2-3x+3=Ax2-Bx+C,则A,B,C的值为( )
| A. | 4,-6,5 | B. | 2,0,-1 | C. | 2,-6,5 | D. | 2,6,5 |
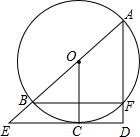 如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$.
如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线交AB的延长线于点E,AD⊥EC,垂足为点D,AD交⊙O于点F,求证:OC平分$\widehat{BF}$. 如图,在△ABC中,AB=AC,AD⊥BC于点D,E,F分别是AC,BC上的点,且∠1+∠2=180°,求证:EF⊥BC.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E,F分别是AC,BC上的点,且∠1+∠2=180°,求证:EF⊥BC.