题目内容
10.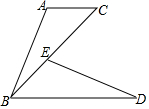 如图,点E在BC上,AC∥BD,AC=BE,BC=BD.
如图,点E在BC上,AC∥BD,AC=BE,BC=BD.(1)说明:△ABC≌△EDB;
(2)若∠C=40°,∠ABC=25°,求∠CED的度数.
分析 (1)根据平行线的性质得到∠C=∠DBE,由全等三角形的判定定理即可得到结论;
(2)根据三角形的内角和得到∠A=115°,根据全等三角形的性质即可得到结论.
解答 解:(1)∵AC∥BD,
∴∠C=∠DBE,
在△ACB与△EBD中,$\left\{\begin{array}{l}{AC=BE}\\{∠C=∠DBE}\\{BC=BD}\end{array}\right.$,
∴△ABC≌△EDB;
(2)∵∠C=40°,∠ABC=25°,
∴∠A=115°,
∵△ABC≌△EDB,
∴∠CED=∠A=115°.
点评 本题考查了全等三角形的判定和性质,三角形的内角和定理,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20.如果+2%表示增加2%,那么-6%表示( )
| A. | 增加14% | B. | 增加6% | C. | 减少6% | D. | 减少26% |
18.对于y=2(x-3)2+2的图象,下列叙述正确的是( )
| A. | 开口向下 | B. | 对称轴为x=3 | ||
| C. | 顶点坐标为(-3,2) | D. | 当x≥3时,y随x增大而减小 |
15.用指定方法解下列一元二次方程.
(1)x2-36=0 (直接开平方法)
(2)x2-4x=2(配方法)
(3)2x2-5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
(1)x2-36=0 (直接开平方法)
(2)x2-4x=2(配方法)
(3)2x2-5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
2.若m•n≠0,则$\frac{|m|}{m}$+$\frac{|n|}{n}$的取值不可能是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
19.下列标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
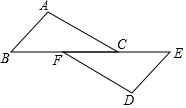 如图,AB=DE,AC=DF,BF=CE;若∠B=50°,∠D=100°,则∠EFD=30°.
如图,AB=DE,AC=DF,BF=CE;若∠B=50°,∠D=100°,则∠EFD=30°.