题目内容
5.巴西世界杯已经打响,目前小组赛正进行得如火如荼,每个小组4个队进行单循环比赛,每场比赛胜队得3分,负队得0分,平局时两队各得1分,小组赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按净胜球排序,净胜球再相同,还有其它方法,直到排出顺序为止.那么理论上,能保证一支球队任何情况下都能出线的最低小组赛积分是( )| A. | 6分 | B. | 7分 | C. | 8分 | D. | 9分 |
分析 易得小组赛的总场数为小组数×(小组数-1)÷2,可得4个队的总积分,进而分类讨论小组得6分或7分能否出线即可.
解答 解:4个队单循环比赛共比赛4×3÷2=6场,每场比赛后两队得分之和或为2分(即打平),或为3分(有胜负),所以6场后各队的得分之和不超过18分,
①若一个队得7分,剩下的3个队得分之和不超过11分,不可能有两个队得分之和大于或等于7分,所以这个队必定出线,
②如果一个队得6分,则有可能还有两个队均得6分,而净胜球比该队多,该队仍不能出线.
故选:B.
点评 本题考查了比赛问题中的推理与论证;得到比赛的总场数以及相应的总积分是解决本题的突破点;分类探讨可以出线的小组的最低分是解决本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.小明在一个矩形的水池里游泳,矩形的长、宽分别为30米、40米,小明在水池中沿直线最远可以游( )
| A. | 30米 | B. | 40米 | C. | 50米 | D. | 60米 |
20.函数y=-$\frac{1}{|x|}$的图象是( )
| A. |  | B. |  | C. |  | D. |  |
17.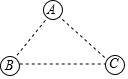 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )| A. | 在三个内角角平分线的交点处 | B. | 在三条高线的交点处 | ||
| C. | 在三条中线的交点处 | D. | 在三条边垂直平分线的交点处 |
14. 如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
 如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )| A. | 始终不变 | B. | 先减小后增大 | C. | 一直变大 | D. | 一直变小 |
15.如图图形是轴对称图形的有( )个


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 |

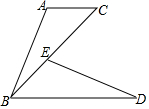 如图,点E在BC上,AC∥BD,AC=BE,BC=BD.
如图,点E在BC上,AC∥BD,AC=BE,BC=BD.