题目内容
2.若m•n≠0,则$\frac{|m|}{m}$+$\frac{|n|}{n}$的取值不可能是( )| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
分析 由于m、n为非零的有理数,根据有理数的分类,m、n的值可以是正数,也可以是负数.那么分三种情况分别讨论:①两个数都是正数;②两个数都是负数;③其中一个数是正数另一个是负数,针对每一种情况,根据绝对值的定义,先去掉绝对值的符号,再计算即可.
解答 解:分3种情况:
①两个数都是正数;
∴$\frac{|m|}{m}$+$\frac{|n|}{n}$=1+1=2,
②两个数都是负数;
∴$\frac{|m|}{m}$+$\frac{|n|}{n}$=-1-1=-2,
③其中一个数是正数另一个是负数,
所以,原式=-1+1=0.
∴$\frac{|m|}{m}$+$\frac{|n|}{n}$的取值不可能是1.
故选B.
点评 此题主要考查了绝对值的定义及有理数的加法法则.由于m、n为非零的有理数,则有3种情况要考虑到,用到了分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.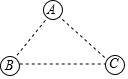 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )| A. | 在三个内角角平分线的交点处 | B. | 在三条高线的交点处 | ||
| C. | 在三条中线的交点处 | D. | 在三条边垂直平分线的交点处 |
14. 如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
 如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )| A. | 始终不变 | B. | 先减小后增大 | C. | 一直变大 | D. | 一直变小 |
11.不能判断两个三个角形全等的条件是( )
| A. | 有两个角及夹边对应相等 | B. | 有两边及夹角对应相等 | ||
| C. | 有三条边对应相等 | D. | 有两边相等的直角三角形 |
12.非零整数a、b满足等式$\sqrt{a}$+$\sqrt{b}$=$\sqrt{48}$,那么a的值为( )
| A. | 3或12 | B. | 12或27 | C. | 40或8 | D. | 3或12或27 |
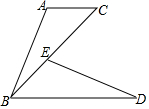 如图,点E在BC上,AC∥BD,AC=BE,BC=BD.
如图,点E在BC上,AC∥BD,AC=BE,BC=BD.


